Question

【題目】如今我們的互聯網生活日益豐富，除了可以很方便地網購，網上叫外賣也開始成為不少人日常生活中不可或缺的一部分.為了解網絡外賣在市的普及情況， 市某調查機構借助網絡進行了關于網絡外賣的問卷調查，并從參與調查的網民中抽取了200人進行抽樣分析，得到表格：（單位：人）

	經常使用網絡外賣	偶爾或不用網絡外賣	合計
男性	50	50	100
女性	60	40	100
合計	110	90	200

（1）根據表中數據，能否在犯錯誤的概率不超過的前提下認為市使用網絡外賣的情況與性別有關？

（2）①現從所抽取的女網民中利用分層抽樣的方法再抽取5人，再從這5人中隨機選出3人贈送外賣優惠券，求選出的3人中至少有2人經常使用網絡外賣的概率；

②將頻率視為概率，從市所有參與調查的網民中隨機抽取10人贈送禮品，記其中經常使用網絡外賣的人數為，求的數學期望和方差.

參考公式： ，其中.

參考數據：

	0.15	0.10	0.05	0.025	0.010
	2.072	2.706	3.841	5.024	6.635

Answer 1

【答案】(1)不能在犯錯誤的概率不超過0.15的前提下認為市使用網絡外賣情況與性別有關；

(2)①；②答案見解析.

【解析】試題分析：

(1)由題意結合列聯表計算可得可知的觀測值 ，所以不能在犯錯誤的概率不超過0.15的前提下認為市使用網絡外賣情況與性別有關；

(2)①依題意可得經常使用網絡外賣的有人，偶爾或不用網絡外賣的有人.則選出的3人中至少有2人經常使用網絡外賣的概率為.

②由題意可得，隨機變量服從二項分布，則； .

試題解析：

（1）由列聯表可知的觀測值 ，

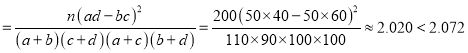所以不能在犯錯誤的概率不超過0.15的前提下認為市使用網絡外賣情況與性別有關.

（2）①依題意，可知所抽取的5名女網民中，經常使用網絡外賣的有（人），

偶爾或不用網絡外賣的有（人）.　

則選出的3人中至少有2人經常使用網絡外賣的概率為.

②由列聯表，可知抽到經常使用網絡外賣的網民的概率為，

將頻率視為概率，即從市市民中任意抽取1人，恰好抽到經常使用網絡外賣的市民的概率為.

由題意得，∴； .