【題目】已知函數
.
(1)若
在
時取到極值,求
的值及
的圖象在
處的切線方程;
(2)若
在
時恒成立,求
的取值范圍.
新課標快樂提優暑假作業陜西旅游出版社系列答案
暑假銜接培優教材浙江工商大學出版社系列答案科目：高中數學 來源： 題型：
【題目】(導學號：05856330)
已知等比數列{an}的前n項和為Sn，且a3＝4，a3，a4＋2，a5成等差數列．數列{
}的前n項和為Tn.
(Ⅰ)求數列{an}的通項公式以及前n項和Sn的表達式；
(Ⅱ)若Tn<m對任意n∈N*恒成立，求實數m的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示，向高為H的水瓶A，B，C，D同時以等速注水，注滿為止；
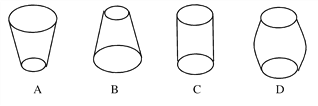
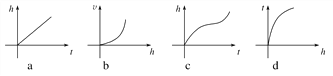
(1)若水深h與注水時間t的函數圖象是下圖中的a，則水瓶的形狀是________；
(2)若水量ν與水深h的函數圖像是下圖中的b，則水瓶的形狀是________；
(3)若水深h與注水時間t的函數圖象是下圖中的c，則水瓶的形狀是________；
(4)若注水時間t與水深h的函數圖象是下圖中的d，則水瓶的形狀是________。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在底面是菱形的四棱錐
中, 
平面
， 
，點
分別為
的中點，設直線
與平面
交于點
.
（1）已知平面
平面
，求證： 
.
（2）求直線
與平面
所成角的正弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】數列
： 
滿足： 
， 
或1（
）．對任意
，都存在
，使得
．，其中
且兩兩不相等．
(I)若
．寫出下列三個數列中所有符合題目條件的數列的序號；
①1,1,1,2,2,2;②1,1,1,1,2,2,2,2;③1,l,1,1,1,2,2,2,2
(Ⅱ)記
．若
，證明： 
；
(Ⅲ)若
，求
的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知棱長為1的正方體ABCD－A1B1C1D1中，E，F，M分別是線段AB、AD、AA1的中點，又P、Q分別在線段A1B1、A1D1上，且A1P＝A1Q＝x(0<x<1).設平面MEF∩平面MPQ
＝l，現有下列結論：
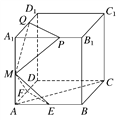
①l∥平面ABCD；
②l⊥AC；
③直線l與平面BCC1B1不垂直；
④當x變化時，l不是定直線.
其中不成立的結論是________.(寫出所有不成立結論的序號)
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設數列
滿足：①
；②所有項
；③ 
．
設集合
，將集合
中的元素的最大值記為
．換句話說， 
是
數列
中滿足不等式
的所有項的項數的最大值．我們稱數列
為數列
的
伴隨數列．例如，數列1,3,5的伴隨數列為1,1,2,2,3．
（1）若數列
的伴隨數列為1,1,1,2,2,2,3，請寫出數列
；
（2）設
，求數列
的伴隨數列
的前100之和；
（3）若數列
的前
項和
（其中
常數），試求數列
的伴隨數列
前
項和
．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
