
【題目】已知平行四邊形ABCD的三個頂點的坐標為A(﹣1,4),B(﹣2,﹣1),C(2,3). 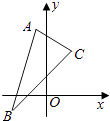
(1)求平行四邊形ABCD的頂點D的坐標
(2)在△ACD中,求CD邊上的高線所在直線方程;
(3)求△ACD的面積.
【答案】
(1)解:由于平行四邊形ABCD的三個頂點的坐標為A(﹣1,4),B(﹣2,﹣1),C(2,3),
設AC的中點為M,則M( ![]() ,
, ![]() ),
),
設點D坐標為(x,y),由已知得M為線段BD中點,有  ,解得
,解得 ![]() ,所以,D(3,8).
,所以,D(3,8).
(2)解:∵直線CD的斜率KCD= ![]() =5,所以CD邊上的高線所在直線的斜率為
=5,所以CD邊上的高線所在直線的斜率為 ![]() ,
,
故△ACD中,CD邊上的高線所在直線的方程為 ![]() ,即為x+5y﹣19=0
,即為x+5y﹣19=0
(3)解:∵C(2,3),D(3,8),∴ ![]() ,
,
由C,D兩點得直線CD的方程為:5x﹣y﹣7=0,∴點A到直線CD的距離為 ![]() =
= ![]() ,
,
∴ ![]()
【解析】(1)設AC的中點為M,則由M為AC的中點求得M( ![]() ,
, ![]() ),設點D坐標為(x,y),由已知得M為線段BD中點,求得D的坐標.(2)求得直線CD的斜率KCD , 可得CD邊上的高線所在直線的斜率為
),設點D坐標為(x,y),由已知得M為線段BD中點,求得D的坐標.(2)求得直線CD的斜率KCD , 可得CD邊上的高線所在直線的斜率為 ![]() ,從而在△ACD中,求得CD邊上的高線所在直線的方程0.(3)求得
,從而在△ACD中,求得CD邊上的高線所在直線的方程0.(3)求得 ![]() ,用兩點式求得直線CD的方程,利用點到直線的距離公式求得點A到直線CD的距離,可得△ACD的面積.
,用兩點式求得直線CD的方程,利用點到直線的距離公式求得點A到直線CD的距離,可得△ACD的面積.


 口算能手系列答案
口算能手系列答案科目:高中數學 來源: 題型:
【題目】函數f(x)(x>0)的導函數為f′(x),若xf′(x)+f(x)=ex , 且f(1)=e,則( )
A.f(x)的最小值為e??
B.f(x)的最大值為e
C.f(x)的最小值為 ![]() ??
??
D.f(x)的最大值為 ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四邊形ABCD中,AB=AD=CD=1,BD= ![]() ,BD⊥CD.將四邊形ABCD沿對角線BD折成四面體A′﹣BCD,使平面A′BD⊥平面BCD,則下列結論正確的是( )
,BD⊥CD.將四邊形ABCD沿對角線BD折成四面體A′﹣BCD,使平面A′BD⊥平面BCD,則下列結論正確的是( ) 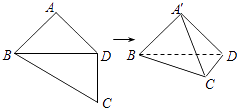
A.A′C⊥BD
B.∠BA′C=90°
C.CA′與平面A′BD所成的角為30°
D.四面體A′﹣BCD的體積為 ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線的中心在原點,焦點F1 , F2在坐標軸上,離心率為 ![]() ,且過點(4,﹣
,且過點(4,﹣ ![]() ),點M(3,m)在雙曲線上.
),點M(3,m)在雙曲線上.
(1)求雙曲線方程;
(2)求證:MF1⊥MF2;
(3)求△F1MF2的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,已知圓C1:x2+y2=16和圓C2:(x﹣7)2+(y﹣4)2=4,
(1)求過點(4,6)的圓C1的切線方程;
(2)設P為坐標平面上的點,且滿足:存在過點P的無窮多對互相垂直的直線l1和l2 , 它們分別與圓C1和圓C2相交,且直線l1被圓C1截得的弦長是直線l2被圓C2截得的弦長的2倍.試求所有滿足條件的點P的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設x取實數,則f(x)與g(x)表示同一個函數的是( )
A.f(x)=x,g(x)= ![]()
B.f(x)= ![]() ,g(x)=
,g(x)= ![]()
C.f(x)=1,g(x)=(x﹣1)0
D.f(x)= ![]() ,g(x)=x﹣3
,g(x)=x﹣3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數y=f(x)定義域是D,若對任意x1 , x2∈D,當x1<x2時,都有f(x1)≤f(x2),則稱函數f(x)在D上為非減函數,設函數y=f(x)在[0,1]上為非減函數,滿足條件:①f(0)=0;②f( ![]() )=
)= ![]() f(x);③f(1﹣x)=1﹣f(x);則f(
f(x);③f(1﹣x)=1﹣f(x);則f( ![]() )+f(
)+f( ![]() )= .
)= .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】二次函數f(x)滿足f(x+1)﹣f(x)=2x,且f(0)=1.
(1)求f(x)的解析式;
(2)在區間[﹣1,1]上,y=f(x)的圖象恒在y=2x+m的圖象上方,試確定實數m的范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com