
【題目】【2017四川瀘州四診】如圖,平面![]() 平面
平面![]() ,四邊形
,四邊形![]() 是菱形,
是菱形, ![]() .
.
(1)求證: ![]() ;
;
(2)若![]() ,且直線
,且直線![]() 與平面
與平面![]() 所成角為
所成角為![]() ,求二面角
,求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
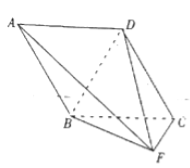
【答案】(1)見解析(2)![]()
【解析】
解:(1)連接![]() ,設
,設![]() ,因為平面
,因為平面![]() 平面
平面![]() ,且交線為
,且交線為![]() ,
,
因為![]() ,所以
,所以![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,四邊形
,四邊形![]() 是菱形,所以
是菱形,所以![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]() ,又
,又![]() ,所以
,所以![]() .
.
(2)解法一:過點![]() 作
作![]() 于點
于點![]() ,連接
,連接![]() ,因為平面
,因為平面![]() 平面
平面![]() ,即直線
,即直線![]() 與平面
與平面![]() 所成角為
所成角為![]() ,不妨設
,不妨設![]() ,則
,則![]() ,過點
,過點![]() 在
在![]() 內作
內作![]() 的平行線
的平行線![]() ,則
,則![]() 平面
平面![]() ,以點
,以點![]() 為原點,分別以
為原點,分別以![]() 所在直線為
所在直線為![]() 軸,建立空間直角坐標系,因為
軸,建立空間直角坐標系,因為![]() ,所以
,所以![]() ,則
,則![]() ,
,
所以![]() ,
,
設平面![]() 的法向量為
的法向量為![]() ,則
,則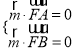 ,所以
,所以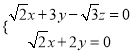 ,取
,取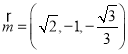 ,
,
同理可得平面![]() 的法向量為
的法向量為![]() ,
,
所以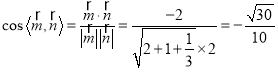 ,因為二面角
,因為二面角![]() 是銳角,所以其余弦值為
是銳角,所以其余弦值為![]() .
.
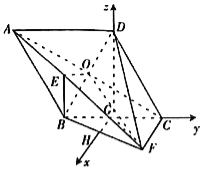
解法二:過點![]() 作
作![]() 于點
于點![]() ,連接
,連接![]() ,因為平面
,因為平面![]() 平面
平面![]() ,又
,又![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]() ,即
,即![]() 平面
平面![]() ,所以
,所以![]() ,即
,即![]() 是二面角
是二面角![]() 的平面角,過點
的平面角,過點![]() 作
作![]() 于點
于點![]() ,連接
,連接![]() ,所以
,所以![]() 平面
平面![]() ,即直線
,即直線![]() 與平面
與平面![]() 所成角為
所成角為![]() ,不妨設
,不妨設![]() ,則
,則![]() ,因為
,因為![]() ∽
∽![]() ,所以
,所以![]() ,又
,又![]() ,所以
,所以![]() ,所以
,所以![]() ,所以二面角
,所以二面角![]() 的余弦值為
的余弦值為![]() .
.


 開心快樂假期作業暑假作業西安出版社系列答案
開心快樂假期作業暑假作業西安出版社系列答案 名題訓練系列答案
名題訓練系列答案科目:高中數學 來源: 題型:
【題目】將函數h(x)=2sin(2x+ ![]() )的圖象向右平移
)的圖象向右平移 ![]() 個單位,再向上平移2個單位,得到函數f(x)的圖象,則函數f(x)的圖象( )
個單位,再向上平移2個單位,得到函數f(x)的圖象,則函數f(x)的圖象( )
A.關于直線x=0對稱
B.關于直線x=π對稱
C.關于點( ![]() ,0)對稱
,0)對稱
D.關于點( ![]() ,2)對稱
,2)對稱
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2017重慶市八中5月模考】已知![]() (
(![]() ),
),![]() ,其中
,其中![]() 為自然對數的底數.
為自然對數的底數.
(1)若![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(2)若在(1)的條件下,當![]() 取最大值時,求證:
取最大值時,求證: ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從某大學一年級女生中,選取身高分別是150cm、155cm、160cm、165cm、170cm的學生各一名,其身高和體重數據如表所示:
身高/cm(x) | 150 | 155 | 160 | 165 | 170 |
體重/kg(y) | 43 | 46 | 49 | 51 | 56 |
(1)求y關于x的線性回歸方程;
(2)利用(1)中的回歸方程,計算身高為168cm時,體重的估計值 ![]() 為多少?
為多少?
參考公式:線性回歸方程 ![]() =
= ![]() x+
x+ ![]() ,其中
,其中 ![]() =
=  =
= 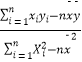 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2017湖南婁底二模】如圖,四棱錐![]() 的底面
的底面![]() 是平行四邊形,側面
是平行四邊形,側面![]() 是邊長為2的正三角形,
是邊長為2的正三角形, ![]()
![]() ,
, ![]() .
.
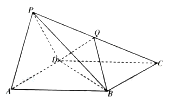
(Ⅰ)求證:平面![]() 平面
平面![]() ;
;
(Ⅱ)設![]() 是棱
是棱![]() 上的點,當
上的點,當![]() 平面
平面![]() 時,求二面角
時,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= 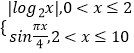 .
.
(1)設函數g(x)=f(x)﹣1,求函數g(x)的零點;
(2)若函數f(x1)=f(x2)=f(x3)=f(x4),且0<x1<x2<x3<x4≤10,求 ![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知在四面體ABCD中,E、F分別是AC、BD的中點,若CD=2AB=4,EF⊥AB,則EF與CD所成的角為( )
A.90°
B.45°
C.60°
D.30°
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,平面四邊形ADEF與梯形ABCD所在的平面互相垂直,AD⊥CD,AD⊥ED,AF∥DE,AB∥CD,CD=2AB=2AD=2ED=xAF.
(Ⅰ)若四點F、B、C、E共面,AB=a,求x的值;
(Ⅱ)求證:平面CBE⊥平面EDB;
(Ⅲ)當x=2時,求二面角F﹣EB﹣C的大小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com