
【題目】如圖所示,正四棱錐P﹣ABCD中,側(cè)棱PA與底面ABCD所成的角的正切值為![]() .
.
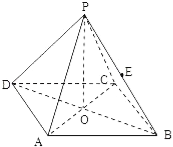
(1)求側(cè)面PAD與底面ABCD所成的二面角的大小;
(2)若E是PB的中點,求異面直線PD與AE所成角的正切值;
(3)問在棱AD上是否存在一點F,使EF⊥側(cè)面PBC,若存在,試確定點F的位置;若不存在,說明理由.
【答案】(1)∠PMO=60°;(2)![]() ;(3)F為四等分點
;(3)F為四等分點
【解析】試題分析:(1)取AD中點M,設(shè)PO⊥面ABCD,連MO、PM,則∠PMO為二面角的平面角,設(shè)AB=a,則可利用tan∠PAO表示出AO和PO,進而根據(jù)![]() 求得tan∠PMO的值,則∠PMO可知.
求得tan∠PMO的值,則∠PMO可知.
(2)連OE,OE∥PD,∠OEA為異面直線PD與AE所成的角.根據(jù)AO⊥BO,AO⊥PO判斷出AO⊥平面PBD,進而可推斷AO⊥OE,進而可知進而可知∠AEO為直線PD與AE所成角,根據(jù)勾股定理求得PD,進而求得OE,則tan∠AEO可求得.
(3)延長MO交BC于N,取PN中點G,連EG、MG.先證出平面PMN和平面PBC垂直,再通過已知條件證出MG⊥平面PBC,取AM中點F,利用EG∥MF,推斷出![]() ,可知EF∥MG.最后可推斷出EF⊥平面PBC.即F為四等分點.
,可知EF∥MG.最后可推斷出EF⊥平面PBC.即F為四等分點.
解:(1)取AD中點M,設(shè)PO⊥面ABCD,連MO、PM,則∠PMO為二面角的平面角,∠PAO為側(cè)棱PA與底面ABCD所成的角,![]() ,
,
設(shè)![]() ,PO=AOtan∠PAO=
,PO=AOtan∠PAO=![]() ,
,![]()
∴∠PMO=60°.
(2)連OE,OE∥PD,∠OEA為異面直線PD與AE所成的角.
 .
.
∵![]()
∴![]()
(3)延長MO交BC于N,取PN中點G,連EG、MG.
![]() .
.
又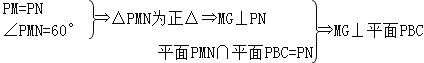
取AM中點F,∵EG∥MF∴![]()
∴EF∥MG.
∴EF⊥平面PBC.
即F為四等分點


 名校課堂系列答案
名校課堂系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】某志愿者到某山區(qū)小學(xué)支教,為了解留守兒童的幸福感,該志愿者對某班40名學(xué)生進行了一次幸福指數(shù)的調(diào)查問卷,并用莖葉圖表示如下(注:圖中幸福指數(shù)低于70,說明孩子幸福感弱;幸福指數(shù)不低于70,說明孩子幸福感強).
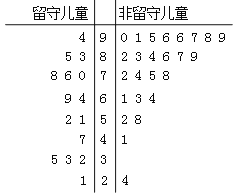
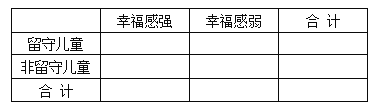
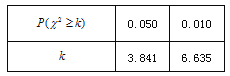
(Ⅰ)根據(jù)莖葉圖中的數(shù)據(jù)完成![]() 列聯(lián)表,并判斷能否有
列聯(lián)表,并判斷能否有![]() 的把握認(rèn)為孩子的幸福感強與是否是留守兒童有關(guān)?
的把握認(rèn)為孩子的幸福感強與是否是留守兒童有關(guān)?
(Ⅱ)從15個留守兒童中按幸福感強弱進行分層抽樣,共抽取5人,又在這5人中隨機抽取2人進行家訪,求這2個學(xué)生中恰有一人幸福感強的概率.
參考公式: 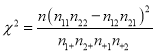 ; 附表:
; 附表:
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知定義在R的奇函數(shù)![]() 滿足
滿足![]() ,且
,且![]() 時,
時, ![]() ,下面四種說法①
,下面四種說法①![]() ;②函數(shù)
;②函數(shù)![]() 在[-6,-2]上是增函數(shù);③函數(shù)
在[-6,-2]上是增函數(shù);③函數(shù)![]() 關(guān)于直線
關(guān)于直線![]() 對稱;④若
對稱;④若![]() ,則關(guān)于
,則關(guān)于![]() 的方程
的方程![]() 在[-8,8]上所有根之和為-8,其中正確的序號__________。
在[-8,8]上所有根之和為-8,其中正確的序號__________。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() ,一直線
,一直線![]() 過點
過點![]() ,
,
①若直線![]() 在兩坐標(biāo)軸上截距之和為12,求直線
在兩坐標(biāo)軸上截距之和為12,求直線![]() 的方程;
的方程;
②若直線![]() 與
與![]() 軸正半軸交于
軸正半軸交于![]() 兩點,當(dāng)
兩點,當(dāng)![]() 面積為
面積為![]() 時求直線
時求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知在多面體ABCDEF中,ABCD為正方形,EF∥平面ABCD,M為FC的中點,AB=2,EF到平面ABCD的距離為2,F(xiàn)C=2.
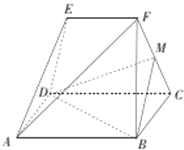
(1)證明:AF∥平面MBD;
(2)若EF=1,求VF﹣MBE.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,其中實數(shù)
,其中實數(shù)![]() .
.
(Ⅰ)判斷![]() 是否為函數(shù)
是否為函數(shù)![]() 的極值點,并說明理由;
的極值點,并說明理由;
(Ⅱ)若![]() 在區(qū)間
在區(qū)間![]() 上恒成立,求
上恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知點![]() 在拋物線
在拋物線![]() :
: ![]() 的準(zhǔn)線上,記
的準(zhǔn)線上,記![]() 的焦點為
的焦點為![]() ,過點
,過點![]() 且與
且與![]() 軸垂直的直線與拋物線交于
軸垂直的直線與拋物線交于![]() ,
, ![]() 兩點,則線段
兩點,則線段![]() 的長為( )
的長為( )
A. 4 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,在![]() 中,
中, ![]() 的中點為
的中點為![]() ,且
,且![]() ,點
,點![]() 在
在![]() 的延長線上,且
的延長線上,且![]() .固定邊
.固定邊![]() ,在平面內(nèi)移動頂點
,在平面內(nèi)移動頂點![]() ,使得圓
,使得圓![]() 與邊
與邊![]() ,邊
,邊![]() 的延長線相切,并始終與
的延長線相切,并始終與![]() 的延長線相切于點
的延長線相切于點![]() ,記頂點
,記頂點![]() 的軌跡為曲線
的軌跡為曲線![]() .以
.以![]() 所在直線為
所在直線為![]() 軸,
軸, ![]() 為坐標(biāo)原點如圖所示建立平面直角坐標(biāo)系.
為坐標(biāo)原點如圖所示建立平面直角坐標(biāo)系.
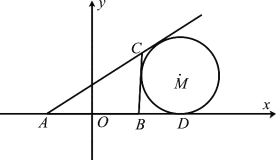
(Ⅰ)求曲線![]() 的方程;
的方程;
(Ⅱ)設(shè)動直線![]() 交曲線
交曲線![]() 于
于![]() 兩點,且以
兩點,且以![]() 為直徑的圓經(jīng)過點
為直徑的圓經(jīng)過點![]() ,求
,求![]() 面積的取值范圍.
面積的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com