小波以游戲方式決定：是去打球、唱歌還是去下棋.游戲規則為：以O為起點,再從A1,A2,A3,A4,A5,A6(如圖)這6個點中任取兩點分別為終點得到兩個向量，記這兩個向量的數量積為X,若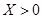
就去打球；若
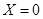就去唱歌；若
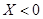就去下棋.
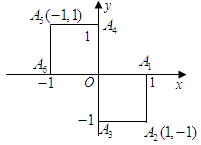
（Ⅰ） 寫出數量積X的所有可能取值;
（Ⅱ）分別求小波去下棋的概率和不去唱歌的概率.
（Ⅰ）
的所有可能取值為
；（Ⅱ）小波去下棋的概率為
，小波不去唱歌的概率
．
解析試題分析：（Ⅰ）的所有可能取值，即從
，
，
，
，
，
這六個向量中任取兩個，共有
種，而對取出兩個向量的數量積進行計算，得到的所有可能取值為；（Ⅱ）求小波去下棋的概率，這顯然是古典概型，只需找出總的事件數有種，因為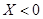就去下棋，只需在（Ⅰ）計算中，找出小于零的次數為
，有古典概型的概率求法知：小波去下棋的概率為 ，小波不去唱歌的概率，它的對立事件為，去唱歌，而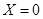就去唱歌，在（Ⅰ）計算中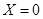，共有四次，故去唱歌的概率為
,有對立事件的概率求法知：小波不去唱歌的概率
．
試題解析：（Ⅰ）由上表可知的所有可能取值為；
、
、
．已知每道工序的加工都相互獨立，三道工序加工的產品都為合格時產品為一等品；有兩次合格為二等品；其它的為廢品，不進入市場．
,每命中一次得1分,沒有命中得0分;向乙靶射擊一次,命中的概率為
,命中得2分,沒有命中得0分.該射手每次射擊的結果相互獨立.假設該射手完成以上三次射擊.
的分布列及數學期望
;
分，負者得
分，比賽進行到有一人比對方多
分或打滿
局時結束.假設選手甲與選手乙比賽時，甲每局獲勝的概率皆為
，且各局比賽勝負互不影響.
局結束，且乙比甲多得
表示比賽停止時已比賽的局數，求隨機變量
，每位學生對每題的選擇是相互獨立的，各學生的選擇相互之間沒有影響.
，求
表示售出A、B商品的日利潤值（單位：元）．將頻率視為概率．
表示第
枚骰子出現的點數，
表示第
枚骰子出現的點數． 
在直線
上的概率； 
的概率．