
【題目】如圖,三棱柱ABC﹣A1B1C1中,側面BB1C1C為菱形,B1C的中點為O,且AO⊥平面BB1C1C. 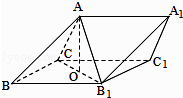
(1)證明:B1C⊥AB;
(2)若AC⊥AB1 , ∠CBB1=60°,BC=1,求三棱柱ABC﹣A1B1C1的高.
【答案】
(1)證明:連接BC1,則O為B1C與BC1的交點,
∵側面BB1C1C為菱形,
∴BC1⊥B1C,
∵AO⊥平面BB1C1C,
∴AO⊥B1C,
∵AO∩BC1=O,
∴B1C⊥平面ABO,
∵AB平面ABO,
∴B1C⊥AB
(2)解:作OD⊥BC,垂足為D,連接AD,作OH⊥AD,垂足為H,

∵BC⊥AO,BC⊥OD,AO∩OD=O,
∴BC⊥平面AOD,
∴OH⊥BC,
∵OH⊥AD,BC∩AD=D,
∴OH⊥平面ABC,
∵∠CBB1=60°,
∴△CBB1為等邊三角形,
∵BC=1,∴OD= ![]() ,
,
∵AC⊥AB1,∴OA= ![]() B1C=
B1C= ![]() ,
,
由OHAD=ODOA,可得AD= ![]() =
= ![]() ,∴OH=
,∴OH= ![]() ,
,
∵O為B1C的中點,
∴B1到平面ABC的距離為 ![]() ,
,
∴三棱柱ABC﹣A1B1C1的高 ![]() .
.
【解析】(1)連接BC1 , 則O為B1C與BC1的交點,證明B1C⊥平面ABO,可得B1C⊥AB;(2)作OD⊥BC,垂足為D,連接AD,作OH⊥AD,垂足為H,證明△CBB1為等邊三角形,求出B1到平面ABC的距離,即可求三棱柱ABC﹣A1B1C1的高.
【考點精析】認真審題,首先需要了解直線與平面垂直的性質(垂直于同一個平面的兩條直線平行).


科目:高中數學 來源: 題型:
【題目】如圖,在△ABC中,已知CA=1,CB=2,∠ACB=60°. 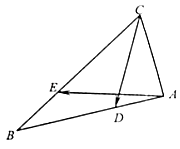
(1)求| ![]() |;
|;
(2)已知點D是AB上一點,滿足 ![]() =λ
=λ ![]() ,點E是邊CB上一點,滿足
,點E是邊CB上一點,滿足 ![]() =λ
=λ ![]() . ①當λ=
. ①當λ= ![]() 時,求
時,求 ![]()
![]() ;
;
②是否存在非零實數λ,使得 ![]() ⊥
⊥ ![]() ?若存在,求出的λ值;若不存在,請說明理由.
?若存在,求出的λ值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知兩矩形ABCD與ADEF所在的平面互相垂直,AB=1,若將△DEF沿直線FD翻折,使得點E落在邊BC上(即點P),則當AD取最小值時,邊AF的長是;此時四面體F﹣ADP的外接球的半徑是 . 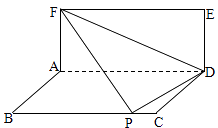
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x﹣alnx(a∈R)
(1)當a=2時,求曲線y=f(x)在點A(1,f(1))處的切線方程;
(2)求函數f(x)的極值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)是定義在R上的偶函數,且在區間(﹣∞,0)上單調遞減,若實數a滿足f(3|2a+1|)>f(﹣ ![]() ),則a的取值范圍是( )
),則a的取值范圍是( )
A.(﹣∞,﹣ ![]() )∪(﹣
)∪(﹣ ![]() ,+∞)
,+∞)
B.(﹣∞,﹣ ![]() )
)
C.(﹣ ![]() ,+∞)
,+∞)
D.(﹣ ![]() ,﹣
,﹣ ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設m,n∈R,若直線(m+1)x+(n+1)y﹣2=0與圓(x﹣1)2+(y﹣1)2=1相切,則m+n的取值范圍是( )
A.[1﹣ ![]() ,1+
,1+ ![]() ]
]
B.(﹣∞,1﹣ ![]() ]∪[1+
]∪[1+ ![]() ,+∞)
,+∞)
C.[2﹣2 ![]() ,2+2
,2+2 ![]() ]
]
D.(﹣∞,2﹣2 ![]() ]∪[2+2
]∪[2+2 ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知全集U=R,集合A={x|x<﹣4,或x>1},B={x|﹣3≤x﹣1≤2}, (Ⅰ)求A∩B、(UA)∪(UB);
(Ⅱ)若{x|2k﹣1≤x≤2k+1}A,求實數k的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com