
【題目】設全集為R,集合A={x| ![]() ≥0},B={x|﹣2≤x<0},則(RA)∩B=( )
≥0},B={x|﹣2≤x<0},則(RA)∩B=( )
A.(﹣1,0)
B.[﹣1,0)
C.[﹣2,﹣1]
D.[﹣2,﹣1)
 輕松課堂單元期中期末專題沖刺100分系列答案
輕松課堂單元期中期末專題沖刺100分系列答案科目:高中數學 來源: 題型:
【題目】甲乙兩人同時生產內徑為![]() 的一種零件,為了對兩人的生產質量進行評比,從他們生產的零件中各抽出 5 件(單位:
的一種零件,為了對兩人的生產質量進行評比,從他們生產的零件中各抽出 5 件(單位: ![]() ) ,
) ,
甲:25.44,25.43, 25.41,25.39,25.38
乙:25.41,25.42, 25.41,25.39,25.42.
從生產的零件內徑的尺寸看、誰生產的零件質量較高.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為矩形,平面
為矩形,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 為
為![]() 中點.
中點.

(Ⅰ)求證: ![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)在棱![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() ?若存在,求
?若存在,求![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知一動點![]() ,
, ![]() 到點
到點![]() 的距離減去它到
的距離減去它到![]() 軸距離的差都是
軸距離的差都是![]() .
.
(![]() )求動點
)求動點![]() 的軌跡方程.
的軌跡方程.
(![]() )設動點
)設動點![]() 的軌跡為
的軌跡為![]() ,已知定點
,已知定點![]() 、
、![]() ,直線
,直線![]() 、
、![]() 與軌跡
與軌跡![]() 的另一個交點分別為
的另一個交點分別為![]() 、
、![]() .
.
(i)點![]() 能否為線段
能否為線段![]() 的中點,若能,求出直線
的中點,若能,求出直線![]() 的方程,若不能,說明理由.
的方程,若不能,說明理由.
(ii)求證:直線![]() 過定點.
過定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,橢圓![]() 的左、右焦點為
的左、右焦點為![]() ,右頂點為
,右頂點為![]() ,上頂點為
,上頂點為![]() ,若
,若![]() ,
, ![]() 與
與![]() 軸垂直,且
軸垂直,且![]() .
.
(1)求橢圓方程;
(2)過點![]() 且不垂直于坐標軸的直線與橢圓交于
且不垂直于坐標軸的直線與橢圓交于![]() 兩點,已知點
兩點,已知點![]() ,當
,當![]() 時,求滿足
時,求滿足![]() 的直線
的直線![]() 的斜率
的斜率![]() 的取值范圍.
的取值范圍.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】橢圓![]() 的離心率是
的離心率是![]() ,過點
,過點![]() 的動直線
的動直線![]() 與橢圓相交于
與橢圓相交于![]() 兩點,當直線
兩點,當直線![]() 與
與![]() 軸平行時,直線
軸平行時,直線![]() 被橢圓
被橢圓![]() 截得的線段長為
截得的線段長為![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)在![]() 軸上是否存在異于點
軸上是否存在異于點![]() 的定點
的定點![]() ,使得直線
,使得直線![]() 變化時,總有
變化時,總有![]() ?若存在,求出點
?若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】統(tǒng)計表明,家庭的月理財投入![]() (單位:千元)與月收入
(單位:千元)與月收入![]() (單位:千元)之間具有線性相關關系.某銀行隨機抽取5個家庭,獲得第
(單位:千元)之間具有線性相關關系.某銀行隨機抽取5個家庭,獲得第![]() (
(![]() )個家庭的月理財投入
)個家庭的月理財投入![]() 與月收入
與月收入![]() 的數據資料,經計算得
的數據資料,經計算得![]() .
.
(1)求![]() 關于
關于![]() 的回歸方程
的回歸方程![]() ;
;
(2)判斷![]() 與
與![]() 之間是正相關還是負相關;
之間是正相關還是負相關;
(3)若某家庭月理財投入為5千元,預測該家庭的月收入.
附:回歸方程的斜率與截距的最小二乘估計公式分別為:
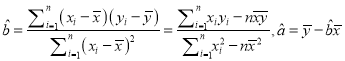 ,其中
,其中![]() 為樣本平均值.
為樣本平均值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知F1 , F2分別為橢圓C: ![]() +
+ ![]() =1(a>b>0)的左、右兩個焦點,橢圓上點M(
=1(a>b>0)的左、右兩個焦點,橢圓上點M( ![]() ,
, ![]() )到F1、F2兩點的距離之和等于4.
)到F1、F2兩點的距離之和等于4.
(1)求橢圓C的方程;
(2)已知過右焦點且垂直于x軸的直線與橢圓交于點N(點N在第一象限),E,F是橢圓C上的兩個動點,如果kEN+KFN=0,證明直線EF的斜率為定值,并求出這個定值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com