【題目】已知
為定義在實數集
上的函數，把方程
稱為函數
的特征方程，特征方程的兩個實根
、
（
），稱為的特征根.
（1）討論函數的奇偶性，并說明理由；
（2）已知
為給定實數，求
的表達式；
（3）把函數
，
的最大值記作
，最小值記作
，研究函數，的單調性，令
，若
恒成立，求
的取值范圍.
能考試期末沖刺卷系列答案科目：高中數學 來源： 題型：
【題目】設集合
是實數集
的子集,如果正實數
滿足:對任意
都存在
使得
則稱為集合的一個“跨度”，已知三個命題:
(1)若為集合的“跨度”,則
也是集合的“跨度”；
(2)集合
的“跨度”的最大值是4；
(3)
是集合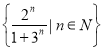
的“跨度”.
這三個命題中正確的個數是（）
A.0B.1C.2D.3
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知A（4，0）、B（1，0），動點M滿足|AM|=2|BM|．
（1）求動點M的軌跡C的方程；
（2）直線l：x+y=4，點N∈l，過N作軌跡C的切線，切點為T，求NT取最小時的切線方程．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，四棱錐P-ABCD中，底面ABCD為矩形，PA⊥平面ABCD，E為PD的中點．
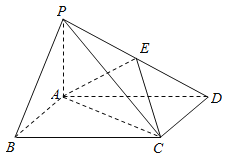
(1) 證明：PB∥平面AEC
(2) 設二面角D-AE-C為60°，AP=1，AD=
，求三棱錐E-ACD的體積
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知兩個無窮數列
分別滿足
，
，
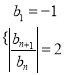其中
，設數列的前
項和分別為
，
（1）若數列都為遞增數列，求數列的通項公式；
（2）若數列
滿足：存在唯一的正整數
（
），使得
，稱數列為“墜點數列”
①若數列
為“5墜點數列”，求
；
②若數列為“
墜點數列”，數列
為“
墜點數列”，是否存在正整數
，使得
，若存在，求的最大值；若不存在，說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
，
，（其中
為自然對數的底數，
…）.
（1）當
時，求函數
的極值；
（2）若函數
在區間
上單調遞增，求
的取值范圍；
（3）若
，當
時，
恒成立，求實數的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知
為正整數且
，將等式
記為
式.
（1）求函數
，
的值域；
（2）試判斷當
時（或2時），是否存在
，
（或，，
）使式成立，若存在，寫出對應，（或，，），若不存在，說明理由；
（3）求所有能使式成立的
（
）所組成的有序實數對
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
