
【題目】已知數(shù)列![]() 滿足
滿足![]() ,
,![]() ,
,![]() 是數(shù)列
是數(shù)列![]() 的前
的前![]() 項的和.
項的和.
(1)求數(shù)列![]() 的通項公式;
的通項公式;
(2)若![]() ,
,![]() ,
,![]() 成等差數(shù)列,
成等差數(shù)列,![]() ,18,
,18,![]() 成等比數(shù)列,求正整數(shù)
成等比數(shù)列,求正整數(shù)![]() 的值;
的值;
(3)是否存在![]() ,使得
,使得![]() 為數(shù)列
為數(shù)列![]() 中的項?若存在,求出所有滿足條件的
中的項?若存在,求出所有滿足條件的![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
【答案】(1)![]() .(2)
.(2)![]() ,
,![]() .(3)
.(3)![]() 或14.
或14.
【解析】試題分析:(1)當![]() 時,
時,![]() ,
,![]() ,當
,當![]() 時,由
時,由![]()
![]()
![]()
![]() 列
列![]() 是首項為2,公差為1的等差數(shù)列
是首項為2,公差為1的等差數(shù)列![]()
![]() .
.
(2)建立方程組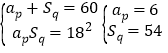 ,或
,或![]() .當
.當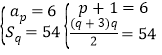
![]()
![]() ,當
,當![]()
![]() 無正整數(shù)解,綜上
無正整數(shù)解,綜上![]() ,
,![]() .
.
(3)假設(shè)存在正整數(shù)![]() ,使得
,使得![]() ,
,![]()
![]()
![]()
![]() ,
,![]() 或
或![]() ,
,![]() ,
,![]() ,
,![]() (舍去)
(舍去)![]()
![]() 或14.
或14.
試題解析:
(1)因為![]() ,
,![]() ,
,
所以當![]() 時,
時,![]() ,
,![]() ,
,
當![]() 時,
時,
由![]()
![]() 和
和![]() ,
,
兩式相除可得,![]() ,即
,即![]()
所以,數(shù)列![]() 是首項為2,公差為1的等差數(shù)列.
是首項為2,公差為1的等差數(shù)列.
于是,![]() .
.
(2)因為![]() ,30,
,30,![]() 成等差數(shù)列,
成等差數(shù)列,![]() ,18,
,18,![]() 成等比數(shù)列,
成等比數(shù)列,
所以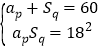 ,于是
,于是![]() ,或
,或![]() .
.
當![]() 時,
時,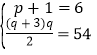 ,解得
,解得![]() ,
,
當![]() 時,
時,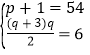 ,無正整數(shù)解,
,無正整數(shù)解,
所以![]() ,
,![]() .
.
(3)假設(shè)存在滿足條件的正整數(shù)![]() ,使得
,使得![]() ,
,
則![]() ,
,
平方并化簡得,![]() ,
,
則![]() ,
,
所以![]() ,或
,或![]() ,或
,或![]() ,
,
解得:![]() ,
,![]() 或
或![]() ,
,![]() ,或
,或![]() ,
,![]() (舍去),
(舍去),
綜上所述,![]() 或14.
或14.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() .
.
(![]() )討論函數(shù)
)討論函數(shù)![]() 在定義域內(nèi)的極值點的個數(shù).
在定義域內(nèi)的極值點的個數(shù).
(![]() )若函數(shù)
)若函數(shù)![]() 在
在![]() 處取得極值,且對
處取得極值,且對![]() ,
,![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
(![]() )當
)當![]() 且
且![]() 時,試比較
時,試比較![]() 與
與![]() 的大小.
的大小.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】(文科學生做)已知數(shù)列![]() 滿足
滿足![]() .
.
(1)求![]() ,
,![]() ,
,![]() 的值,猜想并證明
的值,猜想并證明![]() 的單調(diào)性;
的單調(diào)性;
(2)請用反證法證明數(shù)列![]() 中任意三項都不能構(gòu)成等差數(shù)列.
中任意三項都不能構(gòu)成等差數(shù)列.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖所示,某街道居委會擬在![]() 地段的居民樓正南方向的空白地段
地段的居民樓正南方向的空白地段![]() 上建一個活動中心,其中
上建一個活動中心,其中![]() 米.活動中心東西走向,與居民樓平行. 從東向西看活動中心的截面圖的下部分是長方形
米.活動中心東西走向,與居民樓平行. 從東向西看活動中心的截面圖的下部分是長方形![]() ,上部分是以
,上部分是以![]() 為直徑的半圓. 為了保證居民樓住戶的采光要求,活動中心在與半圓相切的太陽光線照射下落在居民樓上的影長
為直徑的半圓. 為了保證居民樓住戶的采光要求,活動中心在與半圓相切的太陽光線照射下落在居民樓上的影長![]() 不超過
不超過![]() 米,其中該太陽光線與水平線的夾角
米,其中該太陽光線與水平線的夾角![]() 滿足
滿足![]() .
.

(1)若設(shè)計![]() 米,
米,![]() 米,問能否保證上述采光要求?
米,問能否保證上述采光要求?
(2)在保證上述采光要求的前提下,如何設(shè)計![]() 與
與![]() 的長度,可使得活動中心的截面面積最大?(注:計算中
的長度,可使得活動中心的截面面積最大?(注:計算中![]() 取3)
取3)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】執(zhí)行如圖所示的程序框圖,如果運行結(jié)果為720,那么判斷框中應(yīng)填入( ) 
A.k<6?
B.k<7?
C.k>6?
D.k>7?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】數(shù)列{an}滿足a1+a2+a3+…an=2n﹣an(n∈N+).數(shù)列{bn}滿足bn= ![]() ,則{bn}中的最大項的值是 .
,則{bn}中的最大項的值是 .
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】甲、乙、丙三名音樂愛好者參加某電視臺舉辦的演唱技能海選活動,在本次海選中有合格和不合格兩個等級.若海選合格記1分,海選不合格記0分.假設(shè)甲、乙、丙海選合格的概率分別為![]() ,他們海選合格與不合格是相互獨立的.
,他們海選合格與不合格是相互獨立的.
(1)求在這次海選中,這三名音樂愛好者至少有一名海選合格的概率;
(2)記在這次海選中,甲、乙、丙三名音樂愛好者所得分之和為隨機變量![]() ,求隨機變量
,求隨機變量![]() 的分布列和數(shù)學期望
的分布列和數(shù)學期望![]() .
.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com