
設(shè)公差不為0的等差數(shù)列{an}的首項(xiàng)為1,且a2,a5,a14構(gòu)成等比數(shù)列.
(Ⅰ)求數(shù)列{an}的通項(xiàng)公式;
(Ⅱ)若數(shù)列{bn}滿足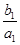 +
+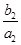 +…+
+…+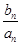 =1-
=1-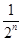 ,n∈N*,求{bn}的前n項(xiàng)和Tn.
,n∈N*,求{bn}的前n項(xiàng)和Tn.
(Ⅰ)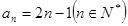 ;(Ⅱ)Tn=3-
;(Ⅱ)Tn=3-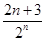 .
.
解析試題分析:(Ⅰ)主要利用等差、等比的概念來求;(Ⅱ)可以構(gòu)造新數(shù)列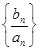 ,則
,則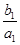 +
+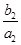 +…+
+…+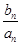 =1-
=1-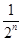 為其前
為其前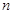 項(xiàng)和,通過
項(xiàng)和,通過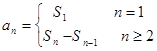 可求數(shù)列
可求數(shù)列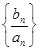 的通項(xiàng)公式,再根據(jù)
的通項(xiàng)公式,再根據(jù)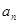 可求
可求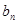 ,然后對其求和;
,然后對其求和;
試題解析:(Ⅰ) 設(shè)等差數(shù)列{an}的公差為d(d≠0),則
∵a2,a5,a14構(gòu)成等比數(shù)列,
∴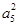 =a2a14,
=a2a14,
即(1+4d)2=(1+d)(1+13d),
解得d=0(舍去),或d=2.
∴an=1+(n-1)×2=2n-1. 4分
(Ⅱ)由已知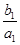 +
+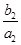 +…+
+…+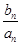 =1-
=1-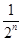 ,n∈N*,
,n∈N*,
當(dāng)n=1時(shí),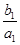 =
= ;
;
當(dāng)n≥2時(shí),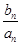 =1-
=1-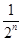 -(1-
-(1-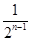 )=
)=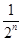 .
.
∴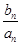 =
=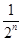 ,n∈N*.
,n∈N*.
由(Ⅰ),知an=2n-1,n∈N*,
∴bn=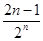 ,n∈N*.
,n∈N*.
又Tn= +
+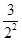 +
+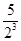 +…+
+…+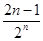 ,
, Tn=
Tn=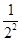 +
+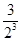 +…+
+…+ +
+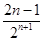 .
.
兩式相減,得 Tn=
Tn= +(
+(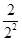 +
+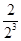 +…+
+…+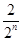 )-
)-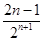 =
=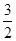 -
-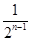 -
-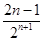 ,
,
∴Tn=3-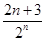 . 12分
. 12分
考點(diǎn):等差、等比的基本概念;錯(cuò)位相減求和.


 口算題卡加應(yīng)用題集訓(xùn)系列答案
口算題卡加應(yīng)用題集訓(xùn)系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知等差數(shù)列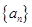 的公差
的公差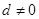 ,它的前
,它的前 項(xiàng)和為
項(xiàng)和為 ,若
,若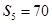 ,且
,且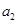 、
、 、
、 成等比數(shù)列.
成等比數(shù)列.
(1)求數(shù)列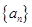 的通項(xiàng)公式;
的通項(xiàng)公式;
(2)設(shè)數(shù)列 的前
的前 項(xiàng)和為
項(xiàng)和為 ,求證:
,求證: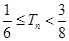 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知等差數(shù)列 滿足:
滿足: ,
, 的前n項(xiàng)和為
的前n項(xiàng)和為 .
.
(1)求 及
及 ;
;
(2)已知數(shù)列 的第n項(xiàng)為
的第n項(xiàng)為 ,若
,若 成等差數(shù)列,且
成等差數(shù)列,且 ,設(shè)數(shù)列
,設(shè)數(shù)列 的前
的前 項(xiàng)和
項(xiàng)和 .求數(shù)列
.求數(shù)列 的前
的前 項(xiàng)和
項(xiàng)和 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知an是一個(gè)等差數(shù)列,且a2=18,a14=—6.
(1)求an的通項(xiàng)an;
(2)求an的前n項(xiàng)和Sn的最大值并求出此時(shí)n值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知等差數(shù)列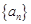 滿足:
滿足: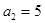 ,
,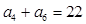 .
.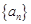 的前n項(xiàng)和為
的前n項(xiàng)和為 .
.
(Ⅰ)求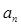 及
及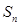 ;
;
(Ⅱ)若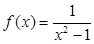 ,
,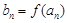 (
(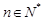 ),求數(shù)列
),求數(shù)列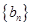 的前
的前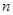 項(xiàng)和
項(xiàng)和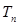 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
設(shè)數(shù)列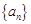 的前n項(xiàng)和為Sn,且
的前n項(xiàng)和為Sn,且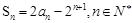 .
.
(1)求數(shù)列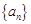 的通項(xiàng)公式;
的通項(xiàng)公式;
(2)令 ,記數(shù)列
,記數(shù)列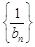 的前
的前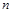 項(xiàng)和為
項(xiàng)和為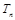 .求證:
.求證: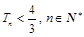 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知各項(xiàng)均為正數(shù)的兩個(gè)無窮數(shù)列 、
、 滿足
滿足 .
.
(Ⅰ)當(dāng)數(shù)列 是常數(shù)列(各項(xiàng)都相等的數(shù)列),且
是常數(shù)列(各項(xiàng)都相等的數(shù)列),且 時(shí),求數(shù)列
時(shí),求數(shù)列 的通項(xiàng)公式;
的通項(xiàng)公式;
(Ⅱ)設(shè) 、
、 都是公差不為0的等差數(shù)列,求證:數(shù)列
都是公差不為0的等差數(shù)列,求證:數(shù)列 有無窮多個(gè),而數(shù)列
有無窮多個(gè),而數(shù)列 惟一確定;
惟一確定;
(Ⅲ)設(shè) ,
, ,求證:
,求證: .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
設(shè) 為等差數(shù)列,
為等差數(shù)列, 為數(shù)列
為數(shù)列 的前
的前 項(xiàng)和,已知
項(xiàng)和,已知 .
.
(Ⅰ)求數(shù)列 的通項(xiàng)公式;
的通項(xiàng)公式;
(Ⅱ)設(shè) ,求數(shù)列
,求數(shù)列 的前
的前 項(xiàng)和
項(xiàng)和 .
.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com