
【題目】如圖是用模擬方法估計(jì)圓周率π的程序框圖,P表示估計(jì)結(jié)果,則圖中空白框內(nèi)應(yīng)填入( ) 
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
【解析】解:法一:由題意以及程序框圖可知,用模擬方法估計(jì)圓周率π的程序框圖,M是圓周內(nèi)的點(diǎn)的次數(shù),當(dāng)i大于1000時, 圓周內(nèi)的點(diǎn)的次數(shù)為4M,總試驗(yàn)次數(shù)為1000,
所以要求的概率 ![]() ,
,
所以空白框內(nèi)應(yīng)填入的表達(dá)式是 ![]() .
.
故選D.
法二:隨機(jī)輸入xi∈(0,1),yi∈(0,1)
那么點(diǎn)P(xi,yi)構(gòu)成的區(qū)域?yàn)橐?/span>
O(0,0),A(1,0),B(1,1),C(0,1)為頂點(diǎn)的正方形.
判斷框內(nèi)x2i+y2i≤1,
若是,說說明點(diǎn)P(xi , yi)在單位圓內(nèi)部( ![]() 圓)內(nèi),并累計(jì)記錄點(diǎn)的個數(shù)M
圓)內(nèi),并累計(jì)記錄點(diǎn)的個數(shù)M
若否,則說明點(diǎn)P(xi , yi)在單位圓內(nèi)部( ![]() 圓)外,并累計(jì)記錄點(diǎn)的個數(shù)N
圓)外,并累計(jì)記錄點(diǎn)的個數(shù)N
第2個判斷框 i>1000,是進(jìn)入計(jì)算
此時落在 ![]() 單位圓內(nèi)的點(diǎn)的個數(shù)為M,一共判斷了1000個點(diǎn)
單位圓內(nèi)的點(diǎn)的個數(shù)為M,一共判斷了1000個點(diǎn)
那么 ![]() 圓的面積/正方形的面積=
圓的面積/正方形的面積= ![]() ,
,
即 ![]() π12÷1=
π12÷1= ![]()
∴π= ![]() (π的估計(jì)值)
(π的估計(jì)值)
即執(zhí)行框內(nèi)計(jì)算的是 ![]() .
.
故選D.
【考點(diǎn)精析】利用算法的循環(huán)結(jié)構(gòu)對題目進(jìn)行判斷即可得到答案,需要熟知在一些算法中,經(jīng)常會出現(xiàn)從某處開始,按照一定條件,反復(fù)執(zhí)行某一處理步驟的情況,這就是循環(huán)結(jié)構(gòu),循環(huán)結(jié)構(gòu)可細(xì)分為兩類:當(dāng)型循環(huán)結(jié)構(gòu)和直到型循環(huán)結(jié)構(gòu).



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為了得到函數(shù) ![]() 的圖象,可以將函數(shù)y=cos2x的圖象( )
的圖象,可以將函數(shù)y=cos2x的圖象( )
A.向左平移 ![]() 個單位長度
個單位長度
B.向左平移 ![]() 個單位長度
個單位長度
C.向右平移 ![]() 個單位長度
個單位長度
D.向右平移 ![]() 個單位長度
個單位長度
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐 ![]() 中,
中, ![]() 底面
底面 ![]() ,
, ![]() ,
, ![]() ,點(diǎn)
,點(diǎn) ![]() 為棱
為棱 ![]() 的中點(diǎn).
的中點(diǎn).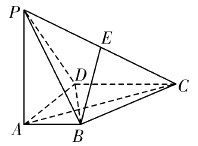
(1)證明: ![]() 面
面 ![]() ;
;
(2)證明 ![]() ;
;
(3)求三棱錐 ![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某校在高二年級開設(shè)選修課,其中數(shù)學(xué)選修課開了三個班.選課結(jié)束后,有四名選修英語的同學(xué)要求改修數(shù)學(xué),但數(shù)學(xué)選修每班至多可再接收兩名同學(xué),那么安排好這四名同學(xué)的方案有( )
A.72種
B.54種
C.36種
D.18種
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在△ABC中,已知AB=2,cosB= ![]() (Ⅰ)若AC=2
(Ⅰ)若AC=2 ![]() ,求sinC的值;
,求sinC的值;
(Ⅱ)若點(diǎn)D在邊AC上,且AD=2DC,BD= ![]() ,求BC的長.
,求BC的長.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在三棱錐P﹣ABC中,PA⊥PC,PB=AB=BC=2,∠ABC=120°, ![]() ,D為AC上一點(diǎn),且AD=3DC.
,D為AC上一點(diǎn),且AD=3DC. 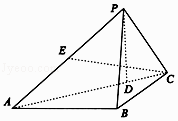
(1)求證:PD⊥平面ABC;
(2)若E為PA中點(diǎn),求直線CE與平面PAB所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)在[0,+∞)上是增函數(shù),g(x)=﹣f(|x|),若g(lgx)>g(1),則x的取值范圍是( )
A.(0,10)
B.(10,+∞)
C.![]()
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知f(x)=2x2+bx+c,不等式f(x)<0的解集為(0,5).
(1)求b,c的值;
(2)若對任意x∈[﹣1,1],不等式f(x)+t≤2恒成立,求t的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系xOy中,點(diǎn)P是圓O:x2+y2=1與x軸正半軸的交點(diǎn),半徑OA在x軸的上方,現(xiàn)將半徑OA繞原點(diǎn)O逆時針旋轉(zhuǎn) ![]() 得到半徑OB.設(shè)∠POA=x(0<x<π),
得到半徑OB.設(shè)∠POA=x(0<x<π), ![]() .
. 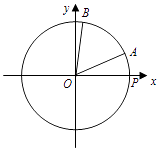
(1)若 ![]() ,求點(diǎn)B的坐標(biāo);
,求點(diǎn)B的坐標(biāo);
(2)求函數(shù)f(x)的最小值,并求此時x的值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com