
【題目】圖1是由正方形![]() ,直角梯形
,直角梯形![]() ,三角形
,三角形![]() 組成的一個平面圖形,其中
組成的一個平面圖形,其中![]() ,
,![]() ,將其沿
,將其沿![]() ,
,![]() 折起使得
折起使得![]() 與
與![]() 重合,連接
重合,連接![]() ,如圖2.
,如圖2.
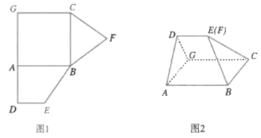
(1)證明:圖2中的![]() ,
,![]() ,
,![]() ,
,![]() 四點共面,且平面
四點共面,且平面![]() 平面
平面![]() ;
;
(2)求圖2中的點![]() 到平面
到平面![]() 的距離.
的距離.
【答案】(1)見解析(2)![]()
【解析】
(1)由平行的傳遞性可證得![]() ,即可說明
,即可說明![]() 四點共面;由
四點共面;由![]() 和直角梯形可知,利用線面垂直的判定定理可證得
和直角梯形可知,利用線面垂直的判定定理可證得![]() 平面
平面![]() ,進而
,進而![]() ,分別在直角梯形
,分別在直角梯形![]() 和直角梯形
和直角梯形![]() 中由勾股定理求得
中由勾股定理求得![]() 和
和![]() ,再由勾股定理逆定理可知
,再由勾股定理逆定理可知![]() ,從而
,從而![]() 平面
平面![]() ,即可證得平面
,即可證得平面![]() 平面
平面![]() .
.
(2)計算等腰直角三角形![]() 中
中![]() 邊上的高,由線面平行的性質可知,點
邊上的高,由線面平行的性質可知,點![]() 到平面
到平面![]() 的距離
的距離![]() ,分別計算三角形
,分別計算三角形![]() 的面積
的面積![]() 和
和![]() 的面積
的面積![]() ,由等體積法
,由等體積法![]() 構建方程,可求得點
構建方程,可求得點![]() 到平面
到平面![]() 的距離
的距離![]() .
.
(1) 證明:因為正方形![]() 中,
中,![]() ,梯形
,梯形![]() 中,
中,![]() , 所以
, 所以![]() ,
,
所以![]() 四點共面;
四點共面;
因為![]() , 所以
, 所以![]() , 因為
, 因為![]() ,
,
所以![]() 平面
平面![]() ,
,
因為![]() 平面
平面![]() , 所以
, 所以![]() ,
,
在直角梯形![]() 中,
中,![]() ,可求得
,可求得![]() ,
,
同理在直角梯形![]() 中,可求得
中,可求得![]() ,
,
又因為![]() ,
,
則![]() ,
,
由勾股定理逆定理可知![]() ,
,
因為![]() , 所以
, 所以![]() 平面
平面![]() ,
,
因為![]() 平面
平面![]() ,
,
故平面![]() 平面
平面![]() , 即平面
, 即平面![]() 平面
平面![]() .
.
(2)在等腰直角三角形![]() 中,
中,![]() 邊上的高為1, 所以點
邊上的高為1, 所以點![]() 到平面
到平面![]() 的距離等于1,
的距離等于1,
因為![]() 與平面
與平面![]() 平行, 所以點
平行, 所以點![]() 到平面
到平面![]() 的距離
的距離![]() ,
,
三角形![]() 的面積
的面積![]() ,
,
![]() 中,
中,![]() 邊上的高為
邊上的高為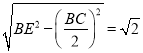 ,
,
又因為![]() 的面積
的面積![]() ,
,
設點![]() 到平面
到平面![]() 的距離為
的距離為![]() ,由三棱錐
,由三棱錐![]() 的體積
的體積![]() ,
,
得![]() , 故點
, 故點![]() 到平面
到平面![]() 的距離為
的距離為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】四川省閬中中學某部根據運動場地的影響,但為盡大可能讓學生都參與到運動會中來,在2018春季運動會中設置了五個項目,其中屬于跑步類的兩項,分別是200米和400米,另外三項分別為跳繩、跳遠、跳高![]() 學校要求每位學生必須參加,且只參加其中一項,學校780名同學參加各運動項目人數統計如下條形圖:
學校要求每位學生必須參加,且只參加其中一項,學校780名同學參加各運動項目人數統計如下條形圖:

其中參加跑步類的人數所占頻率為![]() ,為了了解學生身體健康與參加運動項目之間的關系,用分層抽樣的方法從這780名學生中抽取13人進行分析.
,為了了解學生身體健康與參加運動項目之間的關系,用分層抽樣的方法從這780名學生中抽取13人進行分析.
![]() 1
1![]() 求條形圖中m和n的值以及抽取的13人中參加200米的學生人數;
求條形圖中m和n的值以及抽取的13人中參加200米的學生人數;
![]() 2
2![]() 現從抽取的參加400米和跳繩兩個項目中隨機抽取4人,記其中參加400米跑的學生人數為X,求離散型隨機變量X的分布列與數學期望.
現從抽取的參加400米和跳繩兩個項目中隨機抽取4人,記其中參加400米跑的學生人數為X,求離散型隨機變量X的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在等腰梯形ABCD中,已知AB=AD=CD=1,BC=2,將△ABD沿直線BD翻折成△A′BD,如圖,則直線BA′與CD所成角的取值范圍是( )
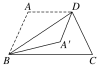
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】京劇是我國的國粹,是“國家級非物質文化遺產”,為紀念著名京劇表演藝術家,京劇藝術大師梅蘭芳先生,某電視臺《我愛京劇》的一期比賽中,2位“梅派”傳人和4位京劇票友(資深業余愛好者)在幕后登臺演唱同一曲目《貴妃醉酒》選段,假設6位演員的演唱水平相當,由現場40位大眾評委和“梅派”傳人的朋友猜測哪兩位是真正的“梅派”傳人.
(1)此欄目編導對本期的40位大眾評委的年齡和對京劇知識的了解進行調查,根據調查得到的數據如下:
京劇票友 | 一般愛好者 | 合計 | |
50歲以上 | 15 | 10 | 25 |
50歲以下 | 3 | 12 | 15 |
合計 | 18 | 22 | 40 |
試問:在犯錯誤的概率不超過多少的前提下,可以認為年齡的大小與對京劇知識的了解有關系?
(2)若在一輪中演唱中,每猜出一位亮相一位,且規定猜出2位“梅派”傳人”或猜出5人后就終止,記本輪競猜一共競猜![]() 次,求隨機變量
次,求隨機變量![]() 的分布列與期望.
的分布列與期望.
參考數據:
0.50 | 0.40 | 0.25 | 0.15 | 0.10 |
0.455 | 0.708 | 1.323 | 2.072 | 2.706 |
0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
參考公式:![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,已知拋物線C:![]() 的焦點為F,過F的直線
的焦點為F,過F的直線![]() 交拋物線C于A,B兩點.
交拋物線C于A,B兩點.
(1)求線段AF的中點M的軌跡方程;
(2)已知△AOB的面積是△BOF面積的3倍,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】變換T1是逆時針旋轉![]() 角的旋轉變換,對應的變換矩陣是M1;變換T2對應的變換矩陣是M2=
角的旋轉變換,對應的變換矩陣是M1;變換T2對應的變換矩陣是M2=![]() .
.
(1)點P(2,1)經過變換T1得到點P',求P'的坐標;
(2)求曲線y=x2先經過變換T1,再經過變換T2所得曲線的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖為廈門市2018年國慶節7天假期的樓房認購量與成交量的折線圖,請你根據折線圖對這7天的認購量(單位:套)與成交量(單位:套),則下列選項中正確的是( )
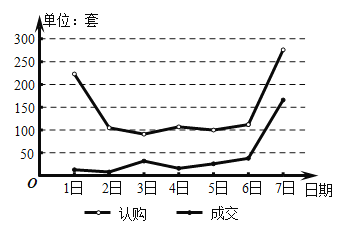
A.日成交量的中位數是10
B.日成交量超過日平均成交量的有2天
C.認購量與日期正相關
D.10月7日認購量的增長率小于10月7日成交量的增長率
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,橢圓C:
中,橢圓C:![]() (
(![]() )的左、右焦點分別為
)的左、右焦點分別為![]() ,
,![]() ,直線l:
,直線l:![]() 交橢圓C于A,B兩點,且
交橢圓C于A,B兩點,且![]() 的周長為8.
的周長為8.
(1)求橢圓C的方程;
(2)若線段![]() 的中點為P,直線
的中點為P,直線![]() 與橢圓C交于M,N兩點,且
與橢圓C交于M,N兩點,且![]() ,求直線l的方程.
,求直線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
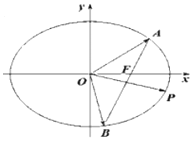
【題目】在平面直角坐標系![]() 中,已知橢圓C:
中,已知橢圓C:![]() (
(![]() >
>![]() >0)的右焦點為F(1,0),且過點(1,
>0)的右焦點為F(1,0),且過點(1,![]() ),過點F且不與
),過點F且不與![]() 軸重合的直線
軸重合的直線![]() 與橢圓C交于A,B兩點,點P在橢圓上,且滿足
與橢圓C交于A,B兩點,點P在橢圓上,且滿足![]() .
.
(1)求橢圓C的標準方程;
(2)若![]() ,求直線AB的方程.
,求直線AB的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com