
【題目】武漢有“九省通衢”之稱,也稱為“江城”,是國家歷史文化名城.其中著名的景點有黃鶴樓、戶部巷、東湖風(fēng)景區(qū)等等.
(1)為了解“五·一”勞動節(jié)當(dāng)日江城某旅游景點游客年齡的分布情況,從年齡在22歲到52歲的游客中隨機(jī)抽取了1000人,制成了如圖的頻率分布直方圖:
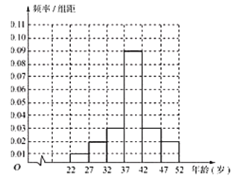
現(xiàn)從年齡在![]() 內(nèi)的游客中,采用分層抽樣的方法抽取10人,再從抽取的10人中隨機(jī)抽取4人,記4人中年齡在
內(nèi)的游客中,采用分層抽樣的方法抽取10人,再從抽取的10人中隨機(jī)抽取4人,記4人中年齡在![]() 內(nèi)的人數(shù)為
內(nèi)的人數(shù)為![]() ,求
,求![]() ;
;
(2)為了給游客提供更舒適的旅游體驗,該旅游景點游船中心計劃在2020年勞動節(jié)當(dāng)日投入至少1艘至多3艘![]() 型游船供游客乘坐觀光.由2010到2019這10年間的數(shù)據(jù)資料顯示每年勞動節(jié)當(dāng)日客流量
型游船供游客乘坐觀光.由2010到2019這10年間的數(shù)據(jù)資料顯示每年勞動節(jié)當(dāng)日客流量![]() (單位:萬人)都大于1.將每年勞動節(jié)當(dāng)日客流量數(shù)據(jù)分成3個區(qū)間整理得表:
(單位:萬人)都大于1.將每年勞動節(jié)當(dāng)日客流量數(shù)據(jù)分成3個區(qū)間整理得表:
勞動節(jié)當(dāng)日客流量 |
|
|
|
頻數(shù)(年) | 2 | 4 | 4 |
以這10年的數(shù)據(jù)資料記錄的3個區(qū)間客流量的頻率作為每年客流量在該區(qū)間段發(fā)生的概率,且每年勞動節(jié)當(dāng)日客流量相互獨立.
該游船中心希望投入的![]() 型游船盡可能被充分利用,但每年勞動節(jié)當(dāng)日
型游船盡可能被充分利用,但每年勞動節(jié)當(dāng)日![]() 型游船最多使用量(單位:艘)要受當(dāng)日客流量
型游船最多使用量(單位:艘)要受當(dāng)日客流量![]() (單位:萬人)的影響,其關(guān)聯(lián)關(guān)系如下表:
(單位:萬人)的影響,其關(guān)聯(lián)關(guān)系如下表:
勞動節(jié)當(dāng)日客流量 |
|
| |
| 1 | 2 | 3 |
若某艘![]() 型游船在勞動節(jié)當(dāng)日被投入且被使用,則游船中心當(dāng)日可獲得利潤3萬元;若某艘
型游船在勞動節(jié)當(dāng)日被投入且被使用,則游船中心當(dāng)日可獲得利潤3萬元;若某艘![]() 型游船勞動節(jié)當(dāng)日被投入?yún)s不被使用,則游船中心當(dāng)日虧損0.5萬元.記
型游船勞動節(jié)當(dāng)日被投入?yún)s不被使用,則游船中心當(dāng)日虧損0.5萬元.記![]() (單位:萬元)表示該游船中心在勞動節(jié)當(dāng)日獲得的總利潤,
(單位:萬元)表示該游船中心在勞動節(jié)當(dāng)日獲得的總利潤,![]() 的數(shù)學(xué)期望越大游船中心在勞動節(jié)當(dāng)日獲得的總利潤越大,問該游船中心在2020年勞動節(jié)當(dāng)日應(yīng)投入多少艘
的數(shù)學(xué)期望越大游船中心在勞動節(jié)當(dāng)日獲得的總利潤越大,問該游船中心在2020年勞動節(jié)當(dāng)日應(yīng)投入多少艘![]() 型游船才能使其當(dāng)日獲得的總利潤最大?
型游船才能使其當(dāng)日獲得的總利潤最大?
【答案】(1)![]() ;(2)投入3艘
;(2)投入3艘![]() 型游船使其當(dāng)日獲得的總利潤最大
型游船使其當(dāng)日獲得的總利潤最大
【解析】
(1)首先計算出在![]() ,
,![]() 內(nèi)抽取的人數(shù),然后利用超幾何分布概率計算公式,計算出
內(nèi)抽取的人數(shù),然后利用超幾何分布概率計算公式,計算出![]() .
.
(2)分別計算出投入![]() 艘游艇時,總利潤的期望值,由此確定當(dāng)日游艇投放量.
艘游艇時,總利潤的期望值,由此確定當(dāng)日游艇投放量.
(1)年齡在![]() 內(nèi)的游客人數(shù)為150,年齡在
內(nèi)的游客人數(shù)為150,年齡在![]() 內(nèi)的游客人數(shù)為100;若采用分層抽樣的方法抽取10人,則年齡在
內(nèi)的游客人數(shù)為100;若采用分層抽樣的方法抽取10人,則年齡在![]() 內(nèi)的人數(shù)為6人,年齡在
內(nèi)的人數(shù)為6人,年齡在![]() 內(nèi)的人數(shù)為4人.
內(nèi)的人數(shù)為4人.
可得![]() .
.
(2)①當(dāng)投入1艘![]() 型游船時,因客流量總大于1,則
型游船時,因客流量總大于1,則![]() (萬元).
(萬元).
②當(dāng)投入2艘![]() 型游船時,
型游船時,
若![]() ,則
,則![]() ,此時
,此時![]() ;
;
若![]() ,則
,則![]() ,此時
,此時![]() ;
;
此時![]() 的分布列如下表:
的分布列如下表:
| 2.5 | 6 |
|
|
|
此時![]() (萬元).
(萬元).
③當(dāng)投入3艘![]() 型游船時,
型游船時,
若![]() ,則
,則![]() ,此時
,此時![]() ;
;
若![]() ,則
,則![]() ,此時
,此時![]() ;
;
若![]() ,則
,則![]() ,此時
,此時![]() ;
;
此時![]() 的分布列如下表:
的分布列如下表:
| 2 | 5.5 | 9 |
|
|
|
|
此時![]() (萬元).
(萬元).
由于![]() ,則該游船中心在2020年勞動節(jié)當(dāng)日應(yīng)投入3艘
,則該游船中心在2020年勞動節(jié)當(dāng)日應(yīng)投入3艘![]() 型游船使其當(dāng)日獲得的總利潤最大.
型游船使其當(dāng)日獲得的總利潤最大.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】德國著名數(shù)學(xué)家狄利克雷(Dirichlet,1805~1859)在數(shù)學(xué)領(lǐng)域成就顯著.19世紀(jì),狄利克雷定義了一個“奇怪的函數(shù)” 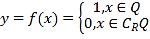 其中R為實數(shù)集,Q為有理數(shù)集.則關(guān)于函數(shù)
其中R為實數(shù)集,Q為有理數(shù)集.則關(guān)于函數(shù)![]() 有如下四個命題,正確的為( )
有如下四個命題,正確的為( )
A.函數(shù)![]() 是偶函數(shù)
是偶函數(shù)
B.![]() ,
,![]() ,
,![]() 恒成立
恒成立
C.任取一個不為零的有理數(shù)T,![]() 對任意的
對任意的![]() 恒成立
恒成立
D.不存在三個點![]() ,
,![]() ,
,![]() ,使得
,使得![]() 為等腰直角三角形
為等腰直角三角形
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知△ABC的內(nèi)角A,B,C的對邊分別為a,b,c,且 ,
,![]() ,
,![]() .
.
(1)求角A的大小;
(2)若a=3,求△ABC的周長L的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】若函數(shù)![]()
![]() 在其定義域內(nèi)有兩個不同的極值點.
在其定義域內(nèi)有兩個不同的極值點.
(1)求實數(shù)![]() 的取值范圍;
的取值范圍;
(2)試比較![]() 與
與![]() 的大小,并說明理由;
的大小,并說明理由;
(3)設(shè)![]() 的兩個極值點為
的兩個極值點為![]() ,
,![]() ,證明:
,證明:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]() .
.
(1)若函數(shù)![]() 在
在![]() 上為減函數(shù),求實數(shù)
上為減函數(shù),求實數(shù)![]() 的最小值;
的最小值;
(2)若存在![]() ,使
,使![]() 成立,求實數(shù)
成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
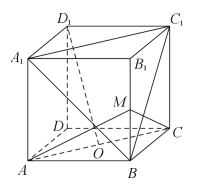
【題目】如圖,正方體![]() 中,
中,![]() 為底面
為底面![]() 的中心,
的中心,![]() 為棱
為棱![]() 的中點,則下列結(jié)論中錯誤的是( )
的中點,則下列結(jié)論中錯誤的是( )
A.![]() 平面
平面![]() B.
B.![]() 平面
平面![]()
C.異面直線![]() 與
與![]() 所成角為
所成角為![]() D.
D.![]() 與底面所成角為
與底面所成角為![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某中學(xué)為了解中學(xué)生的課外閱讀時間,決定在該中學(xué)的1200名男生和800名女生中按分層抽樣的方法抽取20名學(xué)生,對他們的課外閱讀時間進(jìn)行問卷調(diào)查.現(xiàn)在按課外閱讀時間的情況將學(xué)生分成三類:![]() 類(不參加課外閱讀),
類(不參加課外閱讀),![]() 類(參加課外閱讀,但平均每周參加課外閱讀的時間不超過3小時),
類(參加課外閱讀,但平均每周參加課外閱讀的時間不超過3小時),![]() 類(參加課外閱讀,且平均每周參加課外閱讀的時間超過3小時).調(diào)查結(jié)果如下表:
類(參加課外閱讀,且平均每周參加課外閱讀的時間超過3小時).調(diào)查結(jié)果如下表:
|
|
| |
男生 |
| 5 | 3 |
女生 |
| 3 | 3 |
(1)求出表中![]() ,
,![]() 的值;
的值;
(2)根據(jù)表中的統(tǒng)計數(shù)據(jù),完成下面的列聯(lián)表,并判斷是否有90%的把握認(rèn)為“參加課外閱讀與否”與性別有關(guān);
男生 | 女生 | 總計 | ||
不參加課外閱讀 | ||||
參加課外閱讀 | ||||
總計 |
P(K≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】小王想在某市一住宅小區(qū)買套新房,據(jù)了解,該小區(qū)有若干棟互相平行的平頂樓房,每棟樓房有15層,每層樓高為3米,頂樓有1米高的隔熱層,兩樓之間相距60米.小王不想買最前面和最后面的樓房,但希望所買樓層全年每天正午都能曬到太陽.為此,小王查找了有關(guān)地理資料,獲得如下一些信息:①該市的緯度(地面一點所在球半徑與赤道平面所成的角)為北緯![]() ;②正午的太陽直射北回歸線(太陽光線與赤道平面所成的角為
;②正午的太陽直射北回歸線(太陽光線與赤道平面所成的角為![]() )時,物體的影子最短,直射南回歸線(太陽光線與赤道平面所成的角為
)時,物體的影子最短,直射南回歸線(太陽光線與赤道平面所成的角為![]() )時,物體的影子最長,那么小王買房的最低樓層應(yīng)為( )
)時,物體的影子最長,那么小王買房的最低樓層應(yīng)為( )
A.3B.4C.5D.6
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線![]() 的頂點為
的頂點為![]() ,焦點
,焦點![]() .
.

(1)求拋物線![]() 的方程;
的方程;
(2)過![]() 作直線交拋物線于
作直線交拋物線于![]() 、
、![]() 兩點.若直線
兩點.若直線![]() 、
、![]() 分別交直線
分別交直線![]() :
:![]() 于
于![]() 、
、![]() 兩點,求
兩點,求![]() 的最小值.
的最小值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com