
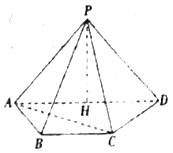
【題目】四棱錐![]() 中,點
中,點![]() 在平面
在平面![]() 內的射影
內的射影![]() 在棱
在棱![]() 上,
上,![]() ,底面
,底面![]() 是梯形,
是梯形,![]() ,且
,且![]() .
.
(1)求證:平面![]() 平面
平面![]() ;
;
(2)若直線![]() 與
與![]() 所成角為60°,求二面角
所成角為60°,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)詳見解析(2)![]()
【解析】
試題分析:(1)證明面面垂直平面![]() 平面
平面![]() ,就是要證線面垂直
,就是要證線面垂直![]() 平面
平面![]() ,其實質還是應用線面垂直判定與性質定理,經多次轉化給予論證:先由射影定義得
,其實質還是應用線面垂直判定與性質定理,經多次轉化給予論證:先由射影定義得![]() 底面
底面![]() ,因而有
,因而有![]() ,再由
,再由![]() ,轉化為
,轉化為![]() 平面
平面![]() (2)利用空間向量求二面角,先根據題意建立空間直角坐標系,設立各點坐標,由直線
(2)利用空間向量求二面角,先根據題意建立空間直角坐標系,設立各點坐標,由直線![]() 與
與![]() 所成角為60°,利用向量數量積確定各點坐標,最后根據方程組求各面法向量,利用向量數量積求兩法向量夾角,進而由二面角與兩法向量關系確定二面角的余弦值.
所成角為60°,利用向量數量積確定各點坐標,最后根據方程組求各面法向量,利用向量數量積求兩法向量夾角,進而由二面角與兩法向量關系確定二面角的余弦值.
試題解析:(1)∵![]() 平面
平面![]() 平面
平面![]() ,∴
,∴![]()
∵![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
(2)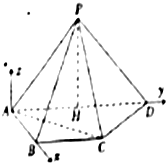
以![]() 為原點,如圖建立空間直角坐標系
為原點,如圖建立空間直角坐標系![]() ,∵
,∵![]() 平面
平面![]() ,
,
∴![]() 軸
軸![]() ,
,
則![]() ,設
,設![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∵![]() 與
與![]() 所成角為60°,
所成角為60°,
∴ ,
,
∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,∵
,∵![]() ,∴
,∴![]() ,∴
,∴![]()
∴![]() ,設平面
,設平面![]() 的法向量為
的法向量為![]() ,
,
由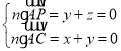 ,得平面
,得平面![]() 的一個法向量為
的一個法向量為![]()
設平面![]() 的法向量為
的法向量為![]() ,
,
由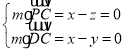 ,得平面
,得平面![]() 的一個法向量為
的一個法向量為![]()
∴![]() ,
,
∵二面角![]() 的平面角為鈍角,
的平面角為鈍角,
∴二面角![]() 的余弦值為
的余弦值為![]()


 期末沖刺100分創新金卷完全試卷系列答案
期末沖刺100分創新金卷完全試卷系列答案科目:高中數學 來源: 題型:
【題目】給出定義在![]() 上的兩個函數
上的兩個函數![]() ,
,![]() .
.
(1)若![]() 在
在![]() 處取最值.求
處取最值.求![]() 的值;
的值;
(2)若函數![]() 在區間
在區間![]() 上單調遞減,求實數
上單調遞減,求實數![]() 的取值范圍;
的取值范圍;
(3)試確定函數![]() 的零點個數,并說明理由.
的零點個數,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線C的頂點在x軸上,兩頂點間的距離是8,離心率![]()
(1)求雙曲線C的標準方程;
(2)過點P(3,0)且斜率為k的直線與雙曲線C有且僅有一個公共點,求k的值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() ,已知
,已知![]() 在
在![]() 處的切線
處的切線![]() 相同.
相同.
(1)求![]() 的值及切線
的值及切線![]() 的方程;
的方程;
(2)設函數![]() ,若存在實數
,若存在實數![]() 使得關于
使得關于![]() 的不等式
的不等式![]() 對
對![]() 上的任意實數
上的任意實數![]() 恒成立,求
恒成立,求![]() 的最小值及對應的
的最小值及對應的![]() 的解析式.
的解析式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知動圓![]() 過定點
過定點![]() ,且與直線
,且與直線![]() 相切,橢圓
相切,橢圓![]() 的對稱軸為坐標軸,
的對稱軸為坐標軸,![]() 點為坐標原點,
點為坐標原點,![]() 是其一個焦點,又點
是其一個焦點,又點![]() 在橢圓
在橢圓![]() 上.
上.
(1)求動圓圓心![]() 的軌跡
的軌跡![]() 的標準方程和橢圓
的標準方程和橢圓![]() 的標準方程;
的標準方程;
(2)若過![]() 的動直線
的動直線![]() 交橢圓
交橢圓![]() 于
于![]() 點,交軌跡
點,交軌跡![]() 于
于![]() 兩點,設
兩點,設![]() 為
為![]() 的面積,
的面積,![]() 為
為![]() 的面積,令
的面積,令![]() 的面積,令
的面積,令![]() ,試求
,試求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】pH值是水溶液的重要理化參數。若溶液中氫離子的濃度為[H![]() ](單位:mol/l),則其pH值為-lg[H
](單位:mol/l),則其pH值為-lg[H![]() ]。在標準溫度和氣壓下,若水溶液pH=7,則溶液為中性,pH<7時為酸性,pH>7時為堿性。例如,甲溶液中氫離子濃度為0.0001mol/l,其pH為-1g 0.0001,即pH=4。已知乙溶液的pH=2,則乙溶液中氫離子濃度為______mol/l。若乙溶液中氫離子濃度是丙溶液的兩千萬倍,則丙溶液的酸堿性為______(填中性、酸性或堿性)。
]。在標準溫度和氣壓下,若水溶液pH=7,則溶液為中性,pH<7時為酸性,pH>7時為堿性。例如,甲溶液中氫離子濃度為0.0001mol/l,其pH為-1g 0.0001,即pH=4。已知乙溶液的pH=2,則乙溶液中氫離子濃度為______mol/l。若乙溶液中氫離子濃度是丙溶液的兩千萬倍,則丙溶液的酸堿性為______(填中性、酸性或堿性)。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com