
【題目】隨著5G商用進程的不斷加快,手機廠商之間圍繞5G用戶的爭奪越來越激烈,5G手機也頻頻降低身價飛人尋常百姓家.某科技公司為了給自己新推出的5G手機定價,隨機抽取了100人進行調查,對其在下一次更換5G手機時,能接受的價格(單位:元)進行了統計,得到結果如下表,已知這100個人能接受的價格都在![]() 之間,并且能接受的價格的平均值為2350元(同一組的數據用該組區間的中點值代替).
之間,并且能接受的價格的平均值為2350元(同一組的數據用該組區間的中點值代替).
分組 | 一 | 二 | 三 | 四 | 五 |
手機價格X(元) |
|
|
|
|
|
頻數 | 10 | x | y | 20 | 20 |
(1)現用分層抽樣的方法從第一、二、三組中隨機抽取6人,將該樣本看成一個總體,從中隨機抽取2人,求其中恰有1人能接受的價格不低于2000元的概率;
(2)若人們對5G手機能接受的價格X近似服從正態分布![]() ,其中
,其中![]() 為樣本平均數
為樣本平均數![]() ,
,![]() 為樣本方差
為樣本方差![]() ,求
,求![]() .
.
附:![]() .若
.若![]() ,則
,則![]() ,
,![]() .
.
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】2018年9月,臺風“山竹”在我國多個省市登陸,造成直接經濟損失達52億元.某青年志愿者組織調查了某地區的50個農戶在該次臺風中造成的直接經濟損失,將收集的數據分成五組:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (單位:元),得到如圖所示的頻率分布直方圖.
(單位:元),得到如圖所示的頻率分布直方圖.
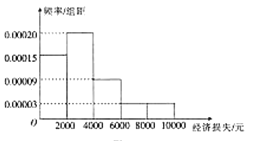
(1)試根據頻率分布直方圖估計該地區每個農戶的平均損失(同一組中的數據用該組區間的中點值代表);
(2)臺風后該青年志愿者與當地政府向社會發出倡議,為該地區的農戶捐款幫扶,現從這50戶并且損失超過4000元的農戶中隨機抽取2戶進行重點幫扶,設抽出損失超過8000元的農戶數為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設f(x)是定義在區間(1,+∞)上的函數,其導函數為![]() .如果存在實數a和函數h(x),其中h(x)對任意的x∈(1,+∞)都有h(x)>0,使得
.如果存在實數a和函數h(x),其中h(x)對任意的x∈(1,+∞)都有h(x)>0,使得![]() =h(x)(x2-ax+1),則稱函數f(x)具有性質P(a).
=h(x)(x2-ax+1),則稱函數f(x)具有性質P(a).
(1)設函數![]() ,其中b為實數.
,其中b為實數.
①求證:函數f(x)具有性質P(a).②求函數f(x)的單調區間.
(2)已知函數g(x)具有性質P(2),給定x1,x2∈(1,+∞),x1<x2.設m為實數, ![]() ,且
,且![]() .若
.若![]() ,求實數m的取值范圍
,求實數m的取值范圍
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某鮮花店根據以往某品種鮮花的銷售記錄,繪制出日銷售量的頻率分布直方圖,如圖所示.將日銷售量落入各組區間的頻率視為概率,且假設每天的銷售量相互獨立.

(1)求在未來的連續4天中,有2天的日銷售量低于100枝且另外2天不低于150枝的概率;
(2)用![]() 表示在未來4天里日銷售量不低于100枝的天數,求隨機變量
表示在未來4天里日銷售量不低于100枝的天數,求隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的離心率
的離心率![]() ,短軸的一個端點到焦點的距離為
,短軸的一個端點到焦點的距離為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)斜率為![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
,![]() 兩點,線段
兩點,線段![]() 的中點在直線
的中點在直線![]() 上,求直線
上,求直線![]() 與
與![]() 軸交點縱坐標的最小值.
軸交點縱坐標的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】利用獨立性檢驗的方法調查高中生性別與愛好某項運動是否有關,通過隨機調查200名高中生是否愛好某項運動,利用![]() 列聯表,由計算可得
列聯表,由計算可得![]() ,參照下表:
,參照下表:
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5,024 | 6.635 | 7.879 | 10.828 |
得到的正確結論是( )
A. 有99%以上的把握認為“愛好該項運動與性別無關”
B. 有99%以上的把握認為“愛好該項運動與性別有關”
C. 在犯錯誤的概率不超過0.5%的前提下,認為“愛好該項運動與性別有關”
D. 在犯錯誤的概率不超過0.5%的前提下,認為“愛好該項運動與性別無關”
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com