
已知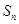 是等差數(shù)列
是等差數(shù)列 的前
的前 項(xiàng)和,且
項(xiàng)和,且 .
.
(1)求 ;
;
(2)令 ,計(jì)算
,計(jì)算 和
和 ,由此推測(cè)數(shù)列
,由此推測(cè)數(shù)列 是等差數(shù)列還是等比數(shù)列,證明你的結(jié)論.
是等差數(shù)列還是等比數(shù)列,證明你的結(jié)論.
(1)an=-1+2(n-1)=2n-3.(2)b1= ,b2=2,b3=8. {bn}是等比數(shù)列.
,b2=2,b3=8. {bn}是等比數(shù)列.
【解析】(1)因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012082413444374387100/SYS201208241345126199359294_DA.files/image002.png">
所以 .
.
(2)因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012082413444374387100/SYS201208241345126199359294_DA.files/image004.png">,所以 ,
,
然后根據(jù)等比數(shù)列的定義證明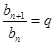 (與n無(wú)關(guān)的常數(shù)即可)
(與n無(wú)關(guān)的常數(shù)即可)
(1)設(shè)數(shù)列{an}的公差為d,那么5a1+ ·5·4d=15. ………………(2分)
·5·4d=15. ………………(2分)
把a(bǔ)1=-1代入上式,得d=2.…………………………………(4分)
因此,an=-1+2(n-1)=2n-3.……………………(6分)
(2)根據(jù) ,得b1=
,得b1= ,b2=2,b3=8.……………(8分)
,b2=2,b3=8.……………(8分)
由此推測(cè){bn}是等比數(shù)列.…………………………(10分)
證明如下:
由(1)得,an+1-an=2,所以 (常數(shù)),
(常數(shù)),


 小夫子全能檢測(cè)系列答案
小夫子全能檢測(cè)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
給出以下幾個(gè)命題,正確的是 .
①函數(shù)![]() 對(duì)稱中心是
對(duì)稱中心是![]() ;
;
②已知![]() 是等差數(shù)列
是等差數(shù)列![]() 的前
的前![]() 項(xiàng)和 ,若
項(xiàng)和 ,若![]() ,則
,則![]() ;
;
③函數(shù)![]() 為奇函數(shù)的充要條件是
為奇函數(shù)的充要條件是![]() ;
;
④已知![]() 均是正數(shù),且
均是正數(shù),且![]() ,則
,則![]() 。
。![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:正定中學(xué)2010高三下學(xué)期第一次考試(數(shù)學(xué)文) 題型:填空題
給出以下幾個(gè)命題,正確的是 .
①函數(shù) 對(duì)稱中心是
對(duì)稱中心是 ;
;
②已知 是等差數(shù)列
是等差數(shù)列 的前
的前 項(xiàng)和,若
項(xiàng)和,若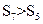 ,則
,則 ;
;
③函數(shù) 為奇函數(shù)的充要條件是
為奇函數(shù)的充要條件是 ;[
;[
④已知 均是正數(shù),且
均是正數(shù),且 ,則
,則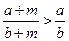 。
。
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2013-2014學(xué)年安徽“江淮十校”協(xié)作體高三上學(xué)期第一次聯(lián)考理數(shù)學(xué)卷(解析版) 題型:解答題
已知 是等差數(shù)列
是等差數(shù)列 的前
的前 項(xiàng)和,滿足
項(xiàng)和,滿足 ;
; 是數(shù)列
是數(shù)列 的前
的前 項(xiàng)和,滿足:
項(xiàng)和,滿足: .
.
(1)求數(shù)列 ,
, 的通項(xiàng)公式;
的通項(xiàng)公式;
(2)求數(shù)列 的前
的前 項(xiàng)和
項(xiàng)和 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2010-2011學(xué)年寧夏高三第四次月考數(shù)學(xué)試(理)題 題型:選擇題
已知 是等差數(shù)列
是等差數(shù)列 的前
的前 項(xiàng)和,且
項(xiàng)和,且 ,
,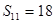 ,則
,則 等于( )
等于( )
A.3 B.5 C.8 D.15
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:黑龍江省哈爾濱市2010屆高三一模數(shù)學(xué)(理)試題 題型:選擇題
已知 是等差數(shù)列
是等差數(shù)列 的前
的前 項(xiàng)和,若
項(xiàng)和,若 ,則
,則 的值是( )
的值是( )
(A)24 (B)42 (C)60 (D)78
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com