【題目】已知點O是四邊形
內(nèi)一點，判斷結(jié)論：“若
，則該四邊形必是矩形，且O為四邊形的中心”是否正確，并說明理由．
【答案】該結(jié)論不正確,見解析
【解析】
設(shè)O是四邊形
內(nèi)一點，過點A作
且
，連接
，過點B作
且
，連接
，
，利用平面向量加法的平行四邊形法則，可證得點O為
與
的中點的連線的中點；同理可證得點O也為
與
的中點的連線的中點，故點O是四邊形對邊中點連線的交點，且該四邊形不一定是矩形.
該結(jié)論不正確．
當(dāng)四邊形是矩形，點O是四邊形的中心時，必有
，反之未必成立．
如圖所示，設(shè)O是四邊形內(nèi)一點，
過點A作且，連接，則四邊形
為平行四邊形，
設(shè)
與的交點為M．過點B作且，連接，，
則四邊形
為平行四邊形，
設(shè)與交于點N，于是M，N分別是，的中點．
∴
，
．又，
∴
，且點O是公共點，點M，N分別在，上，
故M，O，N三點共線，且點O為
的中點，
即點O為與的中點的連線的中點．
同理可證：點O也為與的中點的連線的中點，
∴點O是四邊形對邊中點連線的交點，且該四邊形不一定是矩形．
黃岡小狀元解決問題天天練系列答案
三點一測快樂周計劃系列答案科目：高中數(shù)學(xué) 來源： 題型：
【題目】在平面直角坐標(biāo)系
中，以坐標(biāo)原點
為極點，
軸正半軸為極軸建立極坐標(biāo)系，曲線
的極坐標(biāo)方程為
，
，直線
：
（
為參數(shù)，
）.
（Ⅰ）求直線的普通方程；
（Ⅱ）在曲線上求一點
，使它到直線的距離最短，并求出點的極坐標(biāo).
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知等差數(shù)列{an}滿足a3＝2，前3項和為S3＝
.
(1)求{an}的通項公式；
(2)設(shè)等比數(shù)列{bn}滿足b1＝a1，b4＝a15，求{bn}的前n項和Tn.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】二次函數(shù)圖象上部分點的橫坐標(biāo)x，縱坐標(biāo)y的對應(yīng)值如下表：
x | … | -4 | -3 | -2 | -1 | 0 | 1 | … |
| … | 5 | 0 | -3 | -4 | -3 | m | … |
（1）m= ；
（2）在圖中畫出這個二次函數(shù)的圖象；
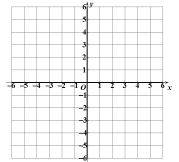
（3）當(dāng)
時，x的取值范圍是 ；
（4）當(dāng)
時，y的取值范圍是 ．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】針對某地區(qū)的一種傳染病與飲用水進(jìn)行抽樣調(diào)查發(fā)現(xiàn):飲用干凈水得病5人，不得病50人；飲用不干凈水得病9人，不得病22人。
（1）作出2×2列聯(lián)表
（2）能否有90％的把握認(rèn)為該地區(qū)中得傳染病與飲用水有關(guān)?
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】現(xiàn)從某醫(yī)院中隨機(jī)抽取了七位醫(yī)護(hù)人員的關(guān)愛患者考核分?jǐn)?shù)（患者考核： 
分制），用相關(guān)的特征量
表示；醫(yī)護(hù)專業(yè)知識考核分?jǐn)?shù)（試卷考試： 
分制），用相關(guān)的特征量
表示，數(shù)據(jù)如下表：
特征量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 98 | 88 | 96 | 91 | 90 | 92 | 96 |
| 9.9 | 8.6 | 9.5 | 9.0 | 9.1 | 9.2 | 9.8 |
（1）求
關(guān)于
的線性回歸方程（計算結(jié)果精確到
）；
（2）利用（1）中的線性回歸方程，分析醫(yī)護(hù)專業(yè)考核分?jǐn)?shù)的變化對關(guān)愛患者考核分?jǐn)?shù)的影響，并估計某醫(yī)護(hù)人員的醫(yī)護(hù)專業(yè)知識考核分?jǐn)?shù)為
分時，他的關(guān)愛患者考核分?jǐn)?shù)（精確到
）；
（3）現(xiàn)要從醫(yī)護(hù)專業(yè)知識考核分?jǐn)?shù)
分以下的醫(yī)護(hù)人員中選派
人參加組建的“九寨溝災(zāi)后醫(yī)護(hù)小分隊”培訓(xùn)，求這兩人中至少有一人考核分?jǐn)?shù)在
分以下的概率.
附：回歸方程
中斜率和截距的最小二乘法估計公式分別為
， 
.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知四邊形
為矩形, 
,
為
的中點,將
沿
折起,得到四棱錐
,設(shè)
的中點為
,在翻折過程中,得到如下有三個命題:
①
平面
，且
的長度為定值
；
②三棱錐
的最大體積為
；
③在翻折過程中，存在某個位置，使得
.
其中正確命題的序號為__________．（寫出所有正確結(jié)論的序號）
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某地發(fā)生地質(zhì)災(zāi)害，使當(dāng)?shù)氐淖詠硭艿搅宋廴荆巢块T對水質(zhì)檢測后，決定往水中投放一種藥劑來凈化水質(zhì)．已知每投放質(zhì)量為m的藥劑后，經(jīng)過x天該藥劑在水中釋放的濃度y（毫克/升）滿足
，其中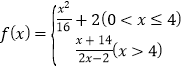
，當(dāng)藥劑在水中釋放的濃度不低于4（毫克/升）時稱為有效凈化；當(dāng)藥劑在水中釋放的濃度不低于4（毫克/升）且不高于10（毫克/升）時稱為最佳凈化．
（1）如果投放的藥劑質(zhì)量為m=4，試問自來水達(dá)到有效凈化一共可持續(xù)幾天？
（2）如果投放的藥劑質(zhì)量為m，為了使在7天（從投放藥劑算起包括7天）之內(nèi)的自來水達(dá)到最佳凈化，試確定應(yīng)該投放的藥劑質(zhì)量m的最小值．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
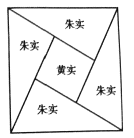
【題目】在古代，直角三角形中較短的直角邊稱為“勾”,較長的直角邊稱為“股”，斜邊稱為“弦”.三國時期吳國數(shù)學(xué)家趙爽用“弦圖”( 如圖) 證明了勾股定理，證明方法敘述為:“按弦圖,又可以勾股相乘為朱實二，倍之為朱實四，以勾股之差自相乘為中黃實，加差實，亦成弦實.”這里的“實”可以理解為面積.這個證明過程體現(xiàn)的是這樣一個等量關(guān)系:“兩條直角邊的乘積是兩個全等直角三角形的面積的和(朱實二 )，4個全等的直角三角形的面積的和(朱實四) 加上中間小正方形的面積(黃實) 等于大正方形的面積(弦實)”. 若弦圖中“弦實”為16，“朱實一”為
,現(xiàn)隨機(jī)向弦圖內(nèi)投入一粒黃豆(大小忽略不計)，則其落入小正方形內(nèi)的概率為( )
A. 
B. 
C. 
D. 
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
