
如圖所示,△VAD是等邊三角形,ABCD是矩形,![]() ,平面VAD⊥平面ABCD,F(xiàn)為AB中點(diǎn)。
,平面VAD⊥平面ABCD,F(xiàn)為AB中點(diǎn)。
(1)求VC與平面ABCD所成角的大小;
(2)當(dāng)V到平面ABCD的距離為3時(shí),求B到平面VFC的距離。
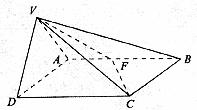
解:解法一:(1)取AD中點(diǎn)E,連接VE、EC,
∵△VAD為等邊三角形,∴ VE⊥AD,
又平面VAD⊥平面ABCD,∴ VE⊥平面ABCD。
∴∠VCE為直線VC與平面ABCD所成的角。
![]()
![]() ,
,
∴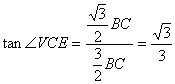 ,∴
,∴![]() 。
。
即直線VC與平面ABCD所成的角為![]() 。
。
(2)∵![]() ,∴
,∴![]() ,
,
∴![]()
![]() 的面積
的面積![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴![]() ,
,
![]() ,
,![]()
即B到平面VFC的距離為![]() 。
。
解法二:取AD中點(diǎn)E,連接VE,EC,取BC中點(diǎn)G,連接EG,設(shè)BC=a,則![]() 。
。
以E為原點(diǎn),![]() 為
為![]() 軸,
軸,![]() 為
為![]() 軸,
軸,![]() 為
為![]() 軸建立空間直角坐標(biāo)系.得:
軸建立空間直角坐標(biāo)系.得:
![]()
則![]() ,
,![]() ,
,![]()
設(shè)面VFC的一個(gè)法向量![]()
∴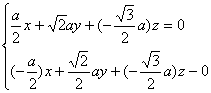
∴![]() ,
,
B到平面VFC的距離為: 。
。



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com