
���}Ŀ����ֱ������(bi��o)ϵ![]() �У�����
�У�����![]() �ą���(sh��)���̞�
�ą���(sh��)���̞�![]() ��
��![]() �酢��(sh��)��
�酢��(sh��)��![]() ������ԭ�c(di��n)
������ԭ�c(di��n)![]() ��O�c(di��n)��
��O�c(di��n)��![]() �S�ķ�ؓ(f��)���S��O�S�����O����(bi��o)ϵ������
�S�ķ�ؓ(f��)���S��O�S�����O����(bi��o)ϵ������![]() �ĘO����(bi��o)���̞�
�ĘO����(bi��o)���̞�![]() ��
��
��1����������![]() ����ͨ���̺�����
����ͨ���̺�����![]() ��ֱ������(bi��o)���̣�
��ֱ������(bi��o)���̣�
��2����֪�c(di��n)![]() ������
������![]() ��һ�c(di��n)�����c(di��n)
��һ�c(di��n)�����c(di��n)![]() ������
������![]() �������x��
�������x��![]() ����
����![]() ��ֵ��
��ֵ��
���𰸡���1��![]() ��
��![]() ����2��
����2��![]() ��
��![]()
��������
��������1��������![]() �ą���(sh��)���̣����ô��뷨��ȥ����(sh��)
�ą���(sh��)���̣����ô��뷨��ȥ����(sh��)![]() ���ɵ�
���ɵ�![]() ����ͨ������������
����ͨ������������![]() �ĘO����(bi��o)���̵�
�ĘO����(bi��o)���̵�![]() �����û�����ʽ�ɵ�
�����û�����ʽ�ɵ�![]() ��ֱ������(bi��o)��������2���O(sh��)����
��ֱ������(bi��o)��������2���O(sh��)����![]() ������һ�c(di��n)
������һ�c(di��n)![]() ��
��![]() ��
��![]() �������c(di��n)��ֱ�����x��ʽ�Y(ji��)���o���ǹ�ʽ�������Ǻ���(sh��)���н��ԿɵýY(ji��)��.
�������c(di��n)��ֱ�����x��ʽ�Y(ji��)���o���ǹ�ʽ�������Ǻ���(sh��)���н��ԿɵýY(ji��)��.
Ԕ������1��������![]() �ą���(sh��)���̣���ȥ����(sh��)
�ą���(sh��)���̣���ȥ����(sh��)![]() ���ɵ�
���ɵ�![]() ����ͨ���̞飺
����ͨ���̞飺![]() ��
��
������![]() �ĘO����(bi��o)���̵�
�ĘO����(bi��o)���̵�![]() ��
��![]() ��
��
������![]() ��ֱ������(bi��o)���̞�
��ֱ������(bi��o)���̞�![]() ��
��
��2���O(sh��)����![]() ������һ�c(di��n)
������һ�c(di��n)![]() ��
��![]() ��
��![]() ���t�c(di��n)
���t�c(di��n)![]() ������
������![]() �ľ��x��
�ľ��x��![]() ��
��
��![]() ����
����![]() ��
��![]() ��
��
��(d��ng)![]() �r(sh��)����
�r(sh��)����![]() ��
��
��(d��ng)![]() �r(sh��)��
�r(sh��)�� ![]() ����
����![]() ��
��![]() ��
��



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��ijУ���˽ⱾУ�W(xu��)����УС�u���������M(f��i)��r���S�C(j��)��ȡ��60���W(xu��)���M(j��n)�нy(t��ng)Ӌ(j��)���õ����ӱ��l��(sh��)�ֲ�����
�����M(f��i)���~����λ��Ԫ�� |
|
|
|
|
|
|
�˔�(sh��) | 30 | 6 | 9 | 10 | 3 | 2 |
ӛ�����M(f��i)���~������300Ԫ�顰�����M(f��i)������֪�ژӱ����S�C(j��)��ȡ1�ˣ��鵽�������������M(f��i)���ĸ��ʞ�![]() .
.
��1���������M(f��i)���~������400Ԫ�ČW(xu��)�����S�C(j��)��ȡ2�ˣ���������1�������M(f��i)���~������500Ԫ�ĸ��ʣ�
��2��Ո(q��ng)�������![]() ��(li��n)���a(b��)�����������Д��Ƿ���
��(li��n)���a(b��)�����������Д��Ƿ���![]() �İ����J(r��n)�顰�����M(f��i)���c����Ů�Ԅe�����P(gu��n)���f������.
�İ����J(r��n)�顰�����M(f��i)���c����Ů�Ԅe�����P(gu��n)���f������.
�����M(f��i) | �Ǹ����M(f��i) | ��Ӌ(j��) | |
���� | |||
�� | 25 | ||
��Ӌ(j��) | 60 |
������R��ֵ��H��������
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
��������ʽ��![]() ������
������![]() ������
������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����(j��)Ϥ,2017������C(j��)����ȫ���Ј�(ch��ng)Ҏ(gu��)ģ���_(d��)��8.19�|��Ԫ,�Ї�(gu��)ռ��(j��)ȫ���Ј�(ch��ng)���~10.8%.ͨ�^��(ji��n)���S�C(j��)��ӵõ�40���Ї�(gu��)�C(j��)����������I(y��),�D��40����I(y��)�C(j��)���˵Įa(ch��n)ֵ�l�ʷֲ�ֱ���D.

��1����![]() ��ֵ��
��ֵ��
��2����������ȡ��40��(g��)��I(y��)����ȡ3��(g��)���鵽�a(ch��n)ֵС��500�fԪ����I(y��)�����^�ɂ�(g��)�ĸ����Ƕ��٣�
��3����������ȡ��40��(g��)��I(y��)����ȡ2��(g��),�O(sh��)![]() ��a(ch��n)ֵ�����^500�fԪ����I(y��)��(g��)��(sh��)�pȥ���^500�fԪ����I(y��)��(g��)��(sh��)�IJ�ֵ,��
��a(ch��n)ֵ�����^500�fԪ����I(y��)��(g��)��(sh��)�pȥ���^500�fԪ����I(y��)��(g��)��(sh��)�IJ�ֵ,��![]() �ķֲ��м�����.
�ķֲ��м�����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪��̖(h��o)����(sh��)sgnx= 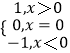 ��f��x����R�ϵ�������(sh��)��g��x��=f��x����f��ax����a��1�����t�� ��
��f��x����R�ϵ�������(sh��)��g��x��=f��x����f��ax����a��1�����t�� ��
A.sgn[g��x��]=sgnx
B.sgn[g��x��]=��sgnx
C.sgn[g��x��]=sgn[f��x��]
D.sgn[g��x��]=��sgn[f��x��]
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
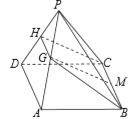
���}Ŀ����D���������F![]() �У�����
�У�����![]() ����Σ�
����Σ�![]() ���߅�����Σ���ƽ��
���߅�����Σ���ƽ��![]() ƽ��
ƽ��![]() .
.![]() ��
��![]() �����c(di��n)��
�����c(di��n)��![]() ��
��![]() �����c(di��n)���^�c(di��n)
�����c(di��n)���^�c(di��n)![]() ��
��![]() ��
��![]() ��ƽ�潻
��ƽ�潻![]() ��
��![]() .
.
��1�����C��![]() ƽ��
ƽ��![]() ��
��
��2����![]() �r(sh��)��������
�r(sh��)��������![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪���}���ٺ���(sh��)![]() ��ֵ����
��ֵ����![]() ��
��
�ڞ��˵õ�����(sh��)![]() �ĈD��ֻ��Ѻ���(sh��)
�ĈD��ֻ��Ѻ���(sh��)![]() �D���ϵ������c(di��n)����ƽ��
�D���ϵ������c(di��n)����ƽ��![]() ��(g��)��λ�L(zh��ng)�ȣ�
��(g��)��λ�L(zh��ng)�ȣ�
�ۮ�(d��ng)![]() ��
��![]() �r(sh��)���纯��(sh��)
�r(sh��)���纯��(sh��)![]() �ĈD����һ�lֱ����
�ĈD����һ�lֱ����
����֪����(sh��) ����
����![]() ������ȣ���
������ȣ���![]() ���t
���t![]() ��ȡֵ������
��ȡֵ������![]() .
.
�������_�����}��(g��)��(sh��)�飨 ��
A. 4 B. 3 C. 2 D. 1
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)f(x)��2x��x��R.
(1)��(d��ng)mȡ��ֵ�r(sh��)������|f(x)��2|��m��һ��(g��)�⣿?j��)ɂ�(g��)�⣿
(2)������ʽ[f(x)]2��f(x)��m>0��R�Ϻ��������m��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��ij��I(y��)푑�(y��ng)ʡ����̖(h��o)�٣���(du��)�F(xi��n)���O(sh��)���M(j��n)�и��죬���˷����O(sh��)�����ǰ���Ч�����F(xi��n)���O(sh��)�����ǰ�����a(ch��n)�Ĵ����a(ch��n)Ʒ�и���ȡ��![]() ���a(ch��n)Ʒ����ӱ����z�y(c��)һ�(xi��ng)�|(zh��)��ָ��(bi��o)ֵ����ԓ�(xi��ng)�|(zh��)��ָ��(bi��o)ֵ����
���a(ch��n)Ʒ����ӱ����z�y(c��)һ�(xi��ng)�|(zh��)��ָ��(bi��o)ֵ����ԓ�(xi��ng)�|(zh��)��ָ��(bi��o)ֵ����![]() ��(n��i)�Įa(ch��n)Ʒҕ��ϸ�Ʒ����t�鲻�ϸ�Ʒ.��D���O(sh��)�����ǰ�Ęӱ����l�ʷֲ�ֱ���D����
��(n��i)�Įa(ch��n)Ʒҕ��ϸ�Ʒ����t�鲻�ϸ�Ʒ.��D���O(sh��)�����ǰ�Ęӱ����l�ʷֲ�ֱ���D����![]() ���O(sh��)������Ęӱ����l��(sh��)�ֲ���.
���O(sh��)������Ęӱ����l��(sh��)�ֲ���.

�����O(sh��)������ӱ����l��(sh��)�ֲ���
�|(zh��)��ָ��(bi��o)ֵ |
|
|
|
|
|
|
�l��(sh��) |
|
|
|
|
|
|
��1����������![]() ��(li��n)�������Д��Ƿ���
��(li��n)�������Д��Ƿ���![]() �İ����J(r��n)��ԓ��I(y��)���a(ch��n)���@�N�a(ch��n)Ʒ���|(zh��)��ָ��(bi��o)ֵ�c�O(sh��)��������P(gu��n)��
�İ����J(r��n)��ԓ��I(y��)���a(ch��n)���@�N�a(ch��n)Ʒ���|(zh��)��ָ��(bi��o)ֵ�c�O(sh��)��������P(gu��n)��
�O(sh��)�����ǰ | �O(sh��)������ | ��Ӌ(j��) | |
�ϸ�Ʒ | |||
���ϸ�Ʒ | |||
��Ӌ(j��) |
��2������(j��)�l�ʷֲ�ֱ���D�ͱ� �ṩ�Ĕ�(sh��)��(j��)��ԇ�Įa(ch��n)Ʒ�ϸ��ʵĽǶȌ�(du��)����ǰ���O(sh��)��ă�(y��u)���M(j��n)�б��^��
��3����I(y��)�����ϸ�Ʒȫ���N������(j��)�͑�����(du��)�ϸ�Ʒ�M(j��n)�е�ӛ��(x��)�֣��|(zh��)��ָ��(bi��o)ֵ����![]() ��(n��i)�Ķ���һ��Ʒ��ÿ���ۃr(ji��)
��(n��i)�Ķ���һ��Ʒ��ÿ���ۃr(ji��)![]() Ԫ���|(zh��)��ָ��(bi��o)ֵ����
Ԫ���|(zh��)��ָ��(bi��o)ֵ����![]() ��
��![]() ��(n��i)�Ķ������Ʒ��ÿ���ۃr(ji��)
��(n��i)�Ķ������Ʒ��ÿ���ۃr(ji��)![]() Ԫ�������ĺϸ�Ʒ��������Ʒ��ÿ���ۃr(ji��)
Ԫ�������ĺϸ�Ʒ��������Ʒ��ÿ���ۃr(ji��)![]() Ԫ.����(j��)��
Ԫ.����(j��)��![]() �Ĕ�(sh��)��(j��)����ԓ�M�ӱ���һ��Ʒ������Ʒ������Ʒ�����ںϸ�Ʒ�е��l�ʴ�������Юa(ch��n)Ʒ�г鵽һ������(y��ng)�ȼ�(j��)�a(ch��n)Ʒ�ĸ���.�F(xi��n)��һ����S�C(j��)ُ�I�ɼ��a(ch��n)Ʒ���O(sh��)��֧�����M(f��i)�Þ�
�Ĕ�(sh��)��(j��)����ԓ�M�ӱ���һ��Ʒ������Ʒ������Ʒ�����ںϸ�Ʒ�е��l�ʴ�������Юa(ch��n)Ʒ�г鵽һ������(y��ng)�ȼ�(j��)�a(ch��n)Ʒ�ĸ���.�F(xi��n)��һ����S�C(j��)ُ�I�ɼ��a(ch��n)Ʒ���O(sh��)��֧�����M(f��i)�Þ�![]() ����λ��Ԫ������
����λ��Ԫ������![]() �ķֲ��к͔�(sh��)�W(xu��)����.
�ķֲ��к͔�(sh��)�W(xu��)����.
����
|
|
|
|
|
|
|
|
|
|
|
|
![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����ֱ������(bi��o)ϵ��(n��i)���c(di��n)![]() ��(sh��)ʩ׃�Q
��(sh��)ʩ׃�Q![]() ��(du��)��(y��ng)�c(di��n)��
��(du��)��(y��ng)�c(di��n)��![]() ���o���������}��
���o���������}��
�وA![]() ������һ�c(di��n)��(sh��)ʩ׃�Q
������һ�c(di��n)��(sh��)ʩ׃�Q![]() ��(du��)��(y��ng)�c(di��n)��܉�E���LjA
��(du��)��(y��ng)�c(di��n)��܉�E���LjA![]() ��
��
����ֱ��![]() ��ÿһ�c(di��n)��(sh��)ʩ׃�Q
��ÿһ�c(di��n)��(sh��)ʩ׃�Q![]() ��(du��)��(y��ng)�c(di��n)��܉�E��������
��(du��)��(y��ng)�c(di��n)��܉�E��������![]() �t
�t![]() ��
��
�ۙE�A![]() ��ÿһ�c(di��n)��(sh��)ʩ׃�Q
��ÿһ�c(di��n)��(sh��)ʩ׃�Q![]() ��(du��)��(y��ng)�c(di��n)��܉�E�����x���ʲ�׃�ęE�A��
��(du��)��(y��ng)�c(di��n)��܉�E�����x���ʲ�׃�ęE�A��
������![]() ��ÿһ�c(di��n)��(sh��)ʩ׃�Q
��ÿһ�c(di��n)��(sh��)ʩ׃�Q![]() ��(du��)��(y��ng)�c(di��n)��܉�E������
��(du��)��(y��ng)�c(di��n)��܉�E������![]() ��
��![]() ������
������![]() �ϵ�����һ�c(di��n)��
�ϵ�����һ�c(di��n)��![]() ������
������![]() �ϵ�����һ�c(di��n)���t
�ϵ�����һ�c(di��n)���t![]() ����Сֵ��
����Сֵ��![]() .
.
�������_���}����̖(h��o)��___________________������ȫ�����_���}����̖(h��o)��.
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com