
已知 ,不等式
,不等式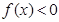 的解集是
的解集是 ,
,
(Ⅰ) 求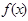 的解析式;
的解析式;
(Ⅱ) 若對(duì)于任意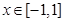 ,不等式
,不等式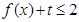 恒成立,求t的取值范圍.
恒成立,求t的取值范圍.

| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
(12分)已知函數(shù) 滿(mǎn)足
滿(mǎn)足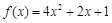 .
.
(1)設(shè) ,求
,求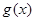 在
在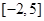 的上的值域;
的上的值域;
(2)設(shè)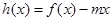 ,在
,在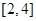 上是單調(diào)函數(shù),求
上是單調(diào)函數(shù),求 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
提高過(guò)江大橋的車(chē)輛通行能力可改善整個(gè)城市的交通狀況.在一般
情況下,大橋上的車(chē)流速度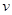 (單位:千米/小時(shí))是車(chē)流密度
(單位:千米/小時(shí))是車(chē)流密度 (單位:輛/千
(單位:輛/千
米)的函數(shù).當(dāng)橋上的車(chē)流密度達(dá)到200輛/千米時(shí),造成堵塞,此時(shí)車(chē)流速度
為0;當(dāng)車(chē)流密度不超過(guò)20輛/千米時(shí),車(chē)流速度為60千米/小時(shí).研究表明:
當(dāng)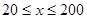 時(shí),車(chē)流速度
時(shí),車(chē)流速度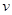 是車(chē)流密度
是車(chē)流密度 的一次函數(shù).
的一次函數(shù).
(Ⅰ)當(dāng)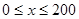 時(shí),求函數(shù)
時(shí),求函數(shù) 的表達(dá)式;
的表達(dá)式;
(Ⅱ)當(dāng)車(chē)流密度 為多大時(shí),車(chē)流量(單位時(shí)間內(nèi)通過(guò)橋上某觀測(cè)點(diǎn)的車(chē)輛數(shù),
為多大時(shí),車(chē)流量(單位時(shí)間內(nèi)通過(guò)橋上某觀測(cè)點(diǎn)的車(chē)輛數(shù),
單位:輛/小時(shí))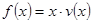 可以達(dá)到最大,并求出最大值.(精確到1輛/小時(shí))
可以達(dá)到最大,并求出最大值.(精確到1輛/小時(shí))
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知奇函數(shù)f(x)=
(1)求實(shí)數(shù)m的值,并在給出的直角坐標(biāo)系中畫(huà)出y=f(x)的圖象;
(2)若函數(shù)f(x)在區(qū)間[-1,a-2]上單調(diào)遞增,試確定a的取值范圍.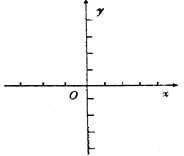
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
.(本小題滿(mǎn)分12分)
某服裝廠生產(chǎn)一種服裝,每件服裝的成本為40元,出廠單價(jià)定為60元.該廠為鼓勵(lì)銷(xiāo)售商訂購(gòu),決定當(dāng)一次訂購(gòu)量超過(guò)100件時(shí),每多訂購(gòu)一件,訂購(gòu)的全部服裝的出廠單價(jià)就降低0.02元.根據(jù)市場(chǎng)調(diào)查,銷(xiāo)售商一次訂購(gòu)量不會(huì)超過(guò)500件.
(1)設(shè)一次訂購(gòu)量為x件,服裝的實(shí)際出廠單價(jià)為P元,寫(xiě)出函數(shù)P=f(x)的表達(dá)式;
(2)當(dāng)銷(xiāo)售商一次訂購(gòu)多少件時(shí),該服裝廠獲得的利潤(rùn)最大,最大利潤(rùn)是多少元?
(服裝廠售出一件服裝的利潤(rùn)=實(shí)際出廠單價(jià) 成本)
成本)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
設(shè)函數(shù)
(1)求函數(shù)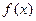 的零點(diǎn);
的零點(diǎn);
(2)在坐標(biāo)系中畫(huà)出函數(shù)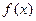 的圖象;
的圖象;
(3)討論方程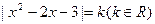 解的情況.
解的情況.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
函數(shù)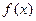 滿(mǎn)足:①定義域是
滿(mǎn)足:①定義域是 ; ②當(dāng)
; ②當(dāng)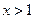 時(shí),
時(shí),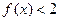 ;
;
③對(duì)任意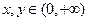 ,總有
,總有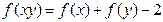
(1)求出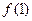 的值;
的值;
(2)判斷函數(shù)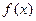 的單調(diào)性,并用單調(diào)性的定義證明你的結(jié)論;
的單調(diào)性,并用單調(diào)性的定義證明你的結(jié)論;
(3)寫(xiě)出一個(gè)滿(mǎn)足上述條件的具體函數(shù)。
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
若二次項(xiàng)系數(shù)為a的二次函數(shù) 同時(shí)滿(mǎn)足如下三個(gè)條件,求
同時(shí)滿(mǎn)足如下三個(gè)條件,求 的解析式.
的解析式.
①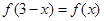 ;②
;② ;③對(duì)任意實(shí)數(shù)
;③對(duì)任意實(shí)數(shù)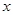 ,都有
,都有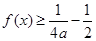 恒成立.
恒成立.
(文) 設(shè)二次函數(shù) 滿(mǎn)足:(1)
滿(mǎn)足:(1)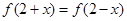 ,(2)被
,(2)被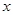 軸截得的弦長(zhǎng)為2,(3)在
軸截得的弦長(zhǎng)為2,(3)在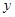 軸截距為6,求此函數(shù)解析式
軸截距為6,求此函數(shù)解析式
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
(本小題滿(mǎn)分14分)已知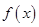 是二次函數(shù),不等式
是二次函數(shù),不等式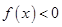 的解集是
的解集是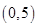 ,且
,且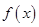 在區(qū)間
在區(qū)間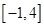 上的最大值是
上的最大值是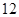 .
.
(1)求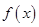 的解析式;
的解析式;
(2)設(shè)函數(shù)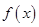 在
在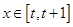 上的最小值為
上的最小值為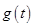 ,求
,求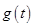 的表達(dá)式.
的表達(dá)式.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com