已知函數f(x)=ax2+bx+c(a,b,c為實數,a≠0),定義域D:[-1,1]
(1)當a=1,b=-1時,若函數f(x)在定義域內恒小于零,求c的取值范圍;
(2)當a=1,常數b<0時,若函數f(x)在定義域內恒不為零,求c的取值范圍;
(3)當b>2a>0時,在D上是否存在x,使得|f(x)|>b成立?(要求寫出推理過程)
解:(1)a=1,b=-1y=x
2-x+c<0在[-1,1]恒成立
則-c>x
2-x在[-1,1]上恒成立
令g(x)=x
2-x,x∈[-1,1],則可得g(x)
max=2
則-c>2即c<-2
(2)a=1,b<0,f(x)=x
2+bx+c≠0在[-1,1]上恒成立?-c≠h(x)=x
2+bx在[-1,1]上恒成立,
而函數h(x)=x
2+bx的對稱軸x=
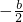
>0
(當
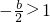
b<-2,函數g(x)在[-1,1]單調遞減,則可得g(1)≤g(x)≤g(-1),即1+b≤g(x)≤1-b
所以,-c>1-b或-c<1+b 所以c<b-1或c>-1-b
(II)當
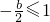
即2≤b<0時,
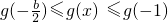
,即
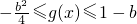
所以
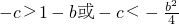
所以,
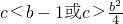
(3)假設在D上存在x,使得|f(x)|>b成立則只要|f(x)|
max>b即可
由于b>2a>0,則對稱軸x=-
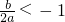
根據二次函數的性質可得|f(x)|的最大值=max{||f(1)|,|f(-1)|}
|a+b+c|>b或|a-b+c|>b
從而可得,存在實數滿足條件
分析:(1)a=1,b=-1y=x
2-x+c<0在[-1,1]恒成立,則-c>x
2-x在[-1,1]上恒成立,令g(x)=x
2-x,x∈[-1,1],-c>g(x)
max可求
(2)a=1,b<0,f(x)=x
2+bx+c≠0在[-1,1]上恒成立?-c≠h(x)=x
2+bx在[-1,1]上恒成立,結合函數h(x)的范圍可求c得范圍
(3)假設在D上存在x,使得|f(x)|>b成立則只要|f(x)|
max>b即可
點評:本題主要考查了二次函數的性質的應用,解題的關鍵是熟練掌握并能靈活利用二次函數的性質及一定的推理與運算的能力

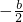 >0
>0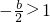 b<-2,函數g(x)在[-1,1]單調遞減,則可得g(1)≤g(x)≤g(-1),即1+b≤g(x)≤1-b
b<-2,函數g(x)在[-1,1]單調遞減,則可得g(1)≤g(x)≤g(-1),即1+b≤g(x)≤1-b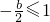 即2≤b<0時,
即2≤b<0時,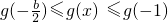 ,即
,即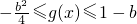
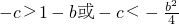
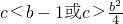
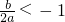


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案