
【題目】為考查某種疫苗預防疾病的效果,進行動物實驗,得到統計數據如下:
未發病 | 發病 | 總計 | |
未注射疫苗 | 20 |
|
|
注射疫苗 | 30 |
|
|
總計 | 50 | 50 | 100 |
現從所有試驗動物中任取一只,取到“注射疫苗”動物的概率為![]() .
.
(1)求![]() 列聯表中的數據
列聯表中的數據![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)能夠有多大把握認為疫苗有效?
(參考公式![]() ,
,![]() )
)
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】定義:對于任意![]() ,
,![]() 仍為數列
仍為數列![]() 中的項,則稱數列
中的項,則稱數列![]() 為“回歸數列”.
為“回歸數列”.
(1)己知![]() (
(![]() ),判斷數列
),判斷數列![]() 是否為“回歸數列”,并說明理由;
是否為“回歸數列”,并說明理由;
(2)若數列![]() 為“回歸數列”,
為“回歸數列”,![]() ,
,![]() ,且對于任意
,且對于任意![]() ,均有
,均有![]() 成立.①求數列
成立.①求數列![]() 的通項公式;②求所有的正整數s,t,使得等式
的通項公式;②求所有的正整數s,t,使得等式![]() 成立.
成立.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】等比數列{an}的各項均為正數,且2a1+3a2=1, ![]() =9a2a6.
=9a2a6.
(1)求數列{an}的通項公式;
(2)設bn=log3a1+log3a2+…+log3an,求數列![]() 的前n項和.
的前n項和.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,以坐標原點為極點,![]() 軸的非負半軸為極軸建立極坐標系,已知曲線
軸的非負半軸為極軸建立極坐標系,已知曲線![]() 的極坐標方程為
的極坐標方程為![]() ,過點
,過點![]() 的直線
的直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),直線
為參數),直線![]() 與曲線
與曲線![]() 相交于
相交于![]() 兩點.
兩點.
(1)寫出曲線![]() 的直角坐標方程和直線
的直角坐標方程和直線![]() 的普通方程;
的普通方程;
(2)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,橢圓![]() :
:![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() 軸,直線
軸,直線![]() 交
交![]() 軸于
軸于![]() 點,
點,![]() ,
,![]() 為橢圓
為橢圓![]() 上的動點,
上的動點,![]() 的面積的最大值為1.
的面積的最大值為1.
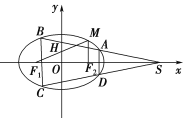
(1)求橢圓![]() 的方程;
的方程;
(2)過點![]() 作兩條直線與橢圓
作兩條直線與橢圓![]() 分別交于
分別交于![]() 且使
且使![]() 軸,如圖,問四邊形
軸,如圖,問四邊形![]() 的兩條對角線的交點是否為定點?若是,求出定點的坐標;若不是,請說明理由.
的兩條對角線的交點是否為定點?若是,求出定點的坐標;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市對創“市級示范性學校”的甲、乙兩所學校進行復查驗收,對辦學的社會滿意度一項評價隨機訪問了20為市民,這20位市民對這兩所學校的評分(評分越高表明市民的評價越好)的數據如下:
甲校:58,66,71,58,67,72,82,92,83,86,67,59,86,72,78,59,68,69,73,81;
乙校:90,80,73,65,67,69,81,85,82,88,89,86,86,78,98,95,96,91,76,69,.
檢查組將成績分成了四個等級:成績在區間![]() 的為
的為![]() 等,在區間
等,在區間![]() 的為
的為![]() 等,在區間
等,在區間![]() 的為
的為![]() 等,在區間
等,在區間![]() 為
為![]() 等.
等.

(1)請用莖葉圖表示上面的數據,并通過觀察莖葉圖,對兩所學校辦學的社會滿意度進行比較,寫出兩個統計結論;
(2)估計哪所學校的市民的評分等級為![]() 級或
級或![]() 級的概率大,說明理由.
級的概率大,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知過原點![]() 的兩條互相垂直的直線與拋物線
的兩條互相垂直的直線與拋物線![]() 相交于不同于原點的兩點
相交于不同于原點的兩點![]() ,且
,且![]() 軸,
軸,![]() 的面積為16.
的面積為16.
(1)求拋物線![]() 的標準方程;
的標準方程;
(2)已知點![]() ,
,![]() ,
,![]() 為拋物線
為拋物線![]() 上不同的三點,若
上不同的三點,若![]() ,試問:直線
,試問:直線![]() 是否過定點?若過定點,求出定點坐標;若不過定點,請說明理由.
是否過定點?若過定點,求出定點坐標;若不過定點,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】小王在年初用50萬元購買一輛大貨車,第一年因繳納各種費用需支出6萬元,從第二年起,每年都比上一年增加支出2萬元,假定該車每年的運輸收入均為25萬元.小王在該車運輸累計收入超過總支出后,考慮將大貨車作為二手車出售,若該車在第x年年底出售,其銷售價格為25-x萬元(國家規定大貨車的報廢年限為10年).
(1)大貨車運輸到第幾年年底,該車運輸累計收入超過總支出?
(2)在第幾年年底將大貨車出售,能使小王獲得的年平均利潤最大(利潤=累計收入+銷售收入-總支出)?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com