
【題目】某租賃公司擁有汽車100輛,當每輛車的月租金為3200元時,可全部租出。當每輛車的月租金每增加50元時(租金增減為50元的整數倍),未租出的車將會增加一輛。租出的車每輛每月需要維護費150元,未租出的車每輛每月需要維護費50元。
(1)當每輛車的月租金定為3600元時,能租出多少輛車?
(2)設租金為(3200+50x)元/輛(x∈N),用x表示租賃公司的月收益y(單位:元)。
(3)當每輛車的月租金定為多少元時,租賃公司的月收益最大?最大月收益是多少?
科目:高中數學 來源: 題型:
【題目】如圖,焦點在x軸的橢圓,離心率e= ![]() ,且過點A(﹣2,1),由橢圓上異于點A的P點發出的光線射到A點處被直線y=1反射后交橢圓于Q點(Q點與P點不重合).
,且過點A(﹣2,1),由橢圓上異于點A的P點發出的光線射到A點處被直線y=1反射后交橢圓于Q點(Q點與P點不重合).
(1)求橢圓標準方程;
(2)求證:直線PQ的斜率為定值;
(3)求△OPQ的面積的最大值. 
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】光線通過一塊玻璃,其強度要損失10%,把幾塊這樣的玻璃重疊起來,設光線原來的強度為![]() ,通過
,通過![]() 塊玻璃以后強度為
塊玻璃以后強度為![]() .
.
(Ⅰ)寫出![]() 關于
關于![]() 的函數關系式;
的函數關系式;
(Ⅱ)通過多少塊玻璃以后,光線強度減弱到原來的![]() 以下.(lg3≈0.4771).
以下.(lg3≈0.4771).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示的多面體是由一個以四邊形ABCD為地面的直四棱柱被平面A1B1C1D1所截面成,若AD=DC=2,AB=BC=2 ![]() ,∠DAB=∠BCD=90°,且AA1=CC1=
,∠DAB=∠BCD=90°,且AA1=CC1= ![]() ;
; 
(1)求二面角D1﹣A1B﹣A的大小;
(2)求此多面體的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】加工爆米花時,爆開且不糊的粒數占加工總粒數的百分比稱為“可食用率”.在特定條件下,可食用率p與加工時間t(單位:分鐘)滿足函數關系![]() (a,b,c是常數),如圖記錄了三次實驗的數據.根據上述函數模型和實驗數據,可以得到最佳加工時間為________分鐘.
(a,b,c是常數),如圖記錄了三次實驗的數據.根據上述函數模型和實驗數據,可以得到最佳加工時間為________分鐘.
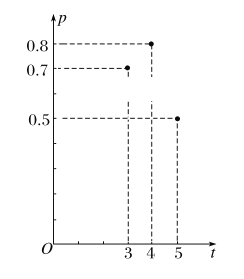
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】橢圓E: ![]() +
+ ![]() =1(a>b>0)的焦點到直線x﹣3y=0的距離為
=1(a>b>0)的焦點到直線x﹣3y=0的距離為 ![]() ,離心率為
,離心率為 ![]() ,拋物線G:y2=2px(p>0)的焦點與橢圓E的焦點重合;斜率為k的直線l過G的焦點與E交于A,B,與G交于C,D.
,拋物線G:y2=2px(p>0)的焦點與橢圓E的焦點重合;斜率為k的直線l過G的焦點與E交于A,B,與G交于C,D.
(1)求橢圓E及拋物線G的方程;
(2)是否存在學常數λ,使 ![]() 為常數,若存在,求λ的值,若不存在,說明理由.
為常數,若存在,求λ的值,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知半徑為![]() 的圓的圓心在
的圓的圓心在![]() 軸上,圓心的橫坐標是整數,且與直線
軸上,圓心的橫坐標是整數,且與直線![]() 相切.
相切.
(Ⅰ)求圓的方程;
(Ⅱ)設直線![]()
![]() 與圓相交于
與圓相交于![]() 兩點,求實數
兩點,求實數![]() 的取值范圍;
的取值范圍;
(Ⅲ) 在(Ⅱ)的條件下,是否存在實數![]() ,使得弦
,使得弦![]() 的垂直平分線
的垂直平分線![]() 過點
過點![]() ,若存在,求出實數
,若存在,求出實數![]() 的值;若不存在,請說明理由
的值;若不存在,請說明理由
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設O是坐標原點,橢圓C:x2+3y2=6的左右焦點分別為F1 , F2 , 且P,Q是橢圓C上不同的兩點,
(1)若直線PQ過橢圓C的右焦點F2 , 且傾斜角為30°,求證:|F1P|、|PQ|、|QF1|成等差數列;
(2)若P,Q兩點使得直線OP,PQ,QO的斜率均存在.且成等比數列.求直線PQ的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2017年,在國家創新驅動戰略下,北斗系統作為一項國家高科技工程,一個開放型的創新平臺,1400多個北斗基站遍布全國,上萬臺套設備組成星地“一張網”,國內定位精度全部達到亞米級,部分地區達到分米級,最高精度甚至可以達到厘米或毫米級。最近北斗三號工程耗資9萬元建成一小型設備,已知這臺設備從啟用的第一天起連續使用,第![]() 天的維修保養費為
天的維修保養費為![]() 元,使用它直至“報廢最合算”(所謂“報廢最合算”是指使用這臺儀器的平均每天耗資最少)為止,一共使用了多少天,平均每天耗資多少錢?
元,使用它直至“報廢最合算”(所謂“報廢最合算”是指使用這臺儀器的平均每天耗資最少)為止,一共使用了多少天,平均每天耗資多少錢?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com