
【題目】在平面直角坐標系xOy中,將從點M出發沿縱、橫方向到達點N的任一路徑稱為M到N的一條“L路徑”.如圖所示的路徑MM1M2M3N與路徑MN1N都是M到N的“L路徑”.某地有三個新建居民區,分別位于平面xOy內三點A(3,20),B(﹣10,0),C(14,0)處.現計劃在x軸上方區域(包含x軸)內的某一點P處修建一個文化中心.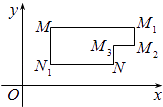
(1)寫出點P到居民區A的“L路徑”長度最小值的表達式(不要求證明);
(2)若以原點O為圓心,半徑為1的圓的內部是保護區,“L路徑”不能進入保護區,請確定點P的位置,使其到三個居民區的“L路徑”長度之和最小.
【答案】
(1)
解:設點P的坐標為(x,y),則
點P到居民區A的“L路徑”長度最小值為|x﹣3|+|y﹣20|,y∈[0,+∞);
(2)
解:由題意知,點P到三個居民區的“L路徑”長度之和的最小值為點P到三個居民區的“L路徑”長度最小值之和(記為d)的最小值
①當y≥1時,d=|x+10|+|x﹣14|+|x﹣3|+2|y|+|y﹣20|
∵d1(x)=|x+10|+|x﹣14|+|x﹣3|≥|x+10|+|x﹣14|≥24
∴當且僅當x=3時,d1(x)=|x+10|+|x﹣14|+|x﹣3|的最小值為24
∵d2(y)=2|y|+|y﹣20|≥21
∴當且僅當y=1時,d2(y)=2|y|+|y﹣20|的最小值為21
∴點P的坐標為(3,1)時,點P到三個居民區的“L路徑”長度之和的最小,且最小值為45;
②當0≤y≤1時,由于“L路徑”不能進入保護區,∴d=|x+10|+|x﹣14|+|x﹣3|+1+|1﹣y|+|y|+|y﹣20|
此時d1(x)=|x+10|+|x﹣14|+|x﹣3|,d2(y)=1+|1﹣y|+|y|+|y﹣20|=22﹣y≥21
由①知d1(x)=|x+10|+|x﹣14|+|x﹣3|≥24,∴d1(x)+d2(y)≥45,當且僅當x=3,y=1時等號成立
綜上所述,在點P(3,1)處修建文化中心,可使該文化中心到三個居民區的“L路徑”長度之和最小.
【解析】(1)根據“L路徑”的定義,可得點P到居民區A的“L路徑”長度最小值;(2)由題意知,點P到三個居民區的“L路徑”長度之和的最小值為點P到三個居民區的“L路徑”長度最小值之和(記為d)的最小值,分類討論,利用絕對值的幾何意義,即可求得點P的坐標.


科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|x﹣1|+|x+a|, ![]()
(1)當a=﹣2時,求不等式f(x)<g(x)的解集;
(2)若a>﹣1,且當x∈[﹣a,1]時,不等式f(x)≤g(x)有解,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列{an}:1,﹣2,﹣2,3,3,3,﹣4,﹣4,﹣4,﹣4,…, ![]() ,…,即當
,…,即當 ![]() <n≤
<n≤ ![]() (k∈N*)時,
(k∈N*)時, ![]() .記Sn=a1+a2+…+an(n∈N).對于l∈N , 定義集合Pl=﹛n|Sn為an的整數倍,n∈N , 且1≤n≤l}
.記Sn=a1+a2+…+an(n∈N).對于l∈N , 定義集合Pl=﹛n|Sn為an的整數倍,n∈N , 且1≤n≤l}
(1)求P11中元素個數;
(2)求集合P2000中元素個數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《厲害了,我的國》這部電影記錄:到2017年底,我國高鐵營運里程達2.5萬公里,位居世界第一位,超過第二名至第十名的總和,約占世界高鐵總量的三分之二.如圖是我國2009年至2017年高鐵營運里程(單位:萬公里)的折線圖.

根據這9年的高鐵營運里程,甲、乙兩位同學分別選擇了![]() 與時間變量
與時間變量![]() 的兩個回歸模型①:
的兩個回歸模型①:![]() ;②
;②![]() .
.
(1)求![]() ,
,![]() (精確到0.01);
(精確到0.01);
(2)乙求得模型②的回歸方程為![]() ,你認為哪個模型的擬合效果更好?并說明理由.
,你認為哪個模型的擬合效果更好?并說明理由.
附:參考公式: ,
,![]() ,
,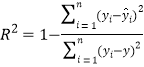 .
.
參考數據:
|
|
|
|
|
|
1.39 | 76.94 | 285 | 0.22 | 0.09 | 3.72 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了了解當下高二男生的身高狀況,某地區對高二年級男生的身高(單位: ![]() )進行了抽樣調查,得到的頻率分布直方圖如圖所示.已知身高在
)進行了抽樣調查,得到的頻率分布直方圖如圖所示.已知身高在![]() 之間的男生人數比身高在
之間的男生人數比身高在![]() 之間的人數少1人.
之間的人數少1人.
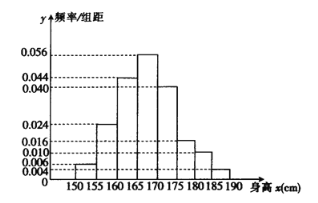
(1)若身高在![]() 以內的定義為身高正常,而該地區共有高二男生18000人,則該地區高二男生中身高正常的大約有多少人?
以內的定義為身高正常,而該地區共有高二男生18000人,則該地區高二男生中身高正常的大約有多少人?
(2)從所抽取的樣本中身高在![]() 和
和![]() 的男生中隨機再選出2人調查其平時體育鍛煉習慣對身高的影響,則所選出的2人中至少有一人身高大于185
的男生中隨機再選出2人調查其平時體育鍛煉習慣對身高的影響,則所選出的2人中至少有一人身高大于185![]() 的概率是多少?
的概率是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知a>0,函數 ![]() .
.
(1)記f(x)在區間[0,4]上的最大值為g(a),求g(a)的表達式;
(2)是否存在a使函數y=f(x)在區間(0,4)內的圖象上存在兩點,在該兩點處的切線互相垂直?若存在,求出a的取值范圍;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個幾何體的三視圖如圖所示,該幾何體從上到下由四個簡單幾何體組成,其體積分別記為V1 , V2 , V3 , V4 , 上面兩個簡單幾何體均為旋轉體,下面兩個簡單幾何體均為多面體,則有( ) 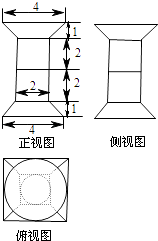
A.V1<V2<V4<V3
B.V1<V3<V2<V4
C.V2<V1<V3<V4
D.V2<V3<V1<V4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某餐廳通過查閱了最近5次食品交易會參會人數![]() (萬人)與餐廳所用原材料數量
(萬人)與餐廳所用原材料數量![]() (袋),得到如下統計表:
(袋),得到如下統計表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
參會人數 | 13 | 9 | 8 | 10 | 12 |
原材料 | 32 | 23 | 18 | 24 | 28 |
(1)根據所給5組數據,求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() .
.
(2)已知購買原材料的費用![]() (元)與數量
(元)與數量![]() (袋)的關系為
(袋)的關系為![]() ,
,
投入使用的每袋原材料相應的銷售收入為700元,多余的原材料只能無償返還,據悉本次交易大會大約有15萬人參加,根據(1)中求出的線性回歸方程,預測餐廳應購買多少袋原材料,才能獲得最大利潤,最大利潤是多少?(注:利潤![]() 銷售收入
銷售收入![]() 原材料費用).
原材料費用).
參考公式:  ,
, ![]() .
.
參考數據: ![]() ,
, ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】閱讀如圖所示的程序框圖,若輸入的k=10,則該算法的功能是( ) 
A.計算數列{2n﹣1}的前10項和
B.計算數列{2n﹣1}的前9項和
C.計算數列{2n﹣1}的前10項和
D.計算數列{2n﹣1}的前9項和
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com