
【題目】若函數![]() 定義域為
定義域為![]() ,且對任意實數
,且對任意實數![]() ,有
,有![]() ,則稱
,則稱![]() 為“
為“![]() 形函數”,若函數
形函數”,若函數![]() 定義域為
定義域為![]() ,函數
,函數![]() 對任意
對任意![]() 恒成立,且對任意實數
恒成立,且對任意實數![]() ,有
,有![]() ,則稱為“對數
,則稱為“對數![]() 形函數” .
形函數” .
(1)試判斷函數![]() 是否為“
是否為“![]() 形函數”,并說明理由;
形函數”,并說明理由;
(2)若![]() 是“對數
是“對數![]() 形函數”,求實數
形函數”,求實數![]() 的取值范圍;
的取值范圍;
(3)若![]() 是“
是“![]() 形函數”,且滿足對任意
形函數”,且滿足對任意![]() ,有
,有![]() ,問
,問![]() 是否為“對數
是否為“對數![]() 形函數”?證明你的結論.
形函數”?證明你的結論.
 期末1卷素質教育評估卷系列答案
期末1卷素質教育評估卷系列答案科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).
為參數).
(1)求曲線![]() 的普通方程;
的普通方程;
(2)經過點![]() (平面直角坐標系
(平面直角坐標系![]() 中點)作直線
中點)作直線![]() 交曲線
交曲線![]() 于
于![]() 兩點,若
兩點,若![]() 恰好為線段的三等分點,求直線
恰好為線段的三等分點,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是我國2008年至2014年生活垃圾無害化處理量(單位:億噸)的折線圖.
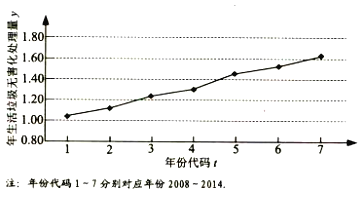
(Ⅰ)由折線圖看出,可用線性回歸模型擬合![]() 與
與![]() 的關系,請用相關系數加以說明;
的關系,請用相關系數加以說明;
(Ⅱ)建立![]() 關于
關于![]() 的回歸方程(系數精確到0.01),預測2016年我國生活垃圾無害化處理量.
的回歸方程(系數精確到0.01),預測2016年我國生活垃圾無害化處理量.
參考數據: ![]() ,
, ![]() ,
, 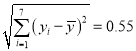 ,
, ![]() .
.
參考公式:相關系數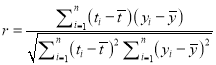 ,
,
回歸方程![]() ,
, 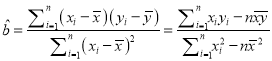 ,
,
本題中斜率和截距的最小二乘估計公式分別為: 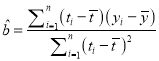 ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,點
中,點![]() ,直線
,直線![]() ,設圓
,設圓![]() 的半徑為1,圓心在
的半徑為1,圓心在![]() 上.
上.
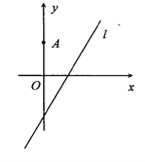
(1)若圓心![]() 也在直線
也在直線![]() 上,過點
上,過點![]() 作圓
作圓![]() 的切線,求切線的方程;
的切線,求切線的方程;
(2)若圓![]() 上存在點
上存在點![]() ,使
,使![]() ,求圓心
,求圓心![]() 的橫坐標
的橫坐標![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1在![]() △
△![]() 中,
中,![]()
![]() ,
,![]() 、
、![]() 分別為線段
分別為線段![]() 、
、![]() 的中點,
的中點,![]() ,
,![]() .以
.以![]() 為折痕,將
為折痕,將![]() △
△![]() 折起到圖2的位置,使平面
折起到圖2的位置,使平面![]() ⊥平面
⊥平面![]() ,連接
,連接![]() ,
,![]() ,設
,設![]() 是線段
是線段![]() 上的動點,滿足
上的動點,滿足![]() .
.
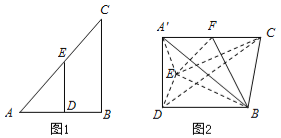
(1)證明:平面![]() ⊥平面
⊥平面![]() ;
;
(2)若二面角![]() 的大小為
的大小為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解某地區某種農產品的年產量![]() (單位:噸)對價格
(單位:噸)對價格![]() (單位:千元/噸)和利潤
(單位:千元/噸)和利潤![]() 的影響,對近五年該農產品的年產量和價格統計如下表:
的影響,對近五年該農產品的年產量和價格統計如下表:

(1)求![]() 關于
關于![]() 的線性回歸方程;
的線性回歸方程;
(2)若每噸該農產品的成本為2千元,假設該農產品可全部賣出,預測當年產量為多少時,年利潤![]() 取到最大值?(結果保留兩位小數)
取到最大值?(結果保留兩位小數)
參考公式: 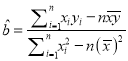 ,
, ![]()
參考數據: ![]() ,
, ![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com