Question

 [番茄花園1] 已知二次函數y=f₁(x)的圖象以原點為頂點且過點(1,1),反比例函數y=f₂(x)的圖象與直線y=x的兩個交點間距離為8,f(x)= f₁(x)+ f₂(x).

 (1) 求函數f(x)的表達式；

(2) 證明:當a>3時,關于x的方程f(x)= f(a)有三個不同的實數解.

 

 

 

---

 [番茄花園1]20．

Answer 1

【答案】

 [番茄花園1] 解：(1)由已知,設f₁(x)=ax²,由f₁(1)=1,得a=1, ∴f₁(x)= x².

   設f₂(x)=(k>0),它的圖象與直線y=x的交點分別為

   A(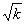,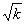)B(－,－)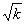

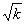   由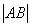=8,得k=8,. ∴f₂(x)=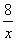.故f(x)=x²+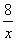.………………………………6分

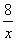     (2) 【證法一】f(x)=f(a),得x²+=a²+,

   即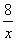=－x²+a²+.

   在同一坐標系內作出f₂(x)=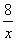和

f₃(x)= －x²+a²+

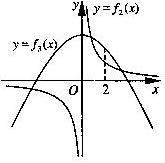
   的大致圖象,其中f₂(x)的圖象是以坐標軸為漸近線,且位于第一、三象限的雙曲線, f₃(x)與的圖象是以(0, a²+)為頂點,開口向下的拋物線.

  因此, f₂(x)與f₃(x)的圖象在第三象限有一個交點,

  即f(x)=f(a)有一個負數解.

  又∵f₂(2)=4, f₃(2)= －4+a²+

   當a>3時,. f₃(2)－f₂(2)= a²+－8>0,

  ∴當a>3時,在第一象限f₃(x)的圖象上存在一點(2,f(2))在f₂(x)圖象的上方.

  ∴f₂(x)與f₃(x)的圖象在第一象限有兩個交點,即f(x)=f(a)有兩個正數解.

  因此,方程f(x)=f(a)有三個實數解. ………………………………14分

  【證法二】由f(x)=f(a),得x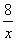²+=a²+,

   即(x－a)(x+a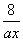－)=0,得方程的一個解x₁=a.

   方程x+a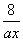－=0化為ax²+a²x－8=0,

   由a>3,△=a⁴+32a>0,得

   x₂=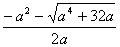, x₃=,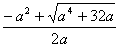

  ∵x₂<0, x₃>0, ∴x₁≠ x₂,且x₂≠ x₃.

  若x₁= x₃,即a=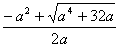,則3a²=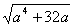, a⁴=4a,

  得a=0或a=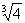,這與a>3矛盾, ∴x₁≠ x₃.

  故原方程f(x)=f(a)有三個實數解.………………………………14分

 

---

 [番茄花園1]20．