Question

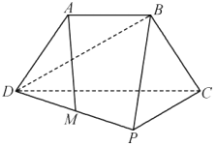
【題目】如圖，三角形PCD所在的平面與等腰梯形ABCD所在的平面垂直，AB＝AD＝CD，AB∥CD，CP⊥CD，M為PD的中點．

（1）求證：AM∥平面PBC；

（2）求證：BD⊥平面PBC．

Answer 1

【答案】（1）見解析（2）見解析

【解析】

（1）取的中點，連，，可證得四邊形為平行四邊形，于是，然后根據(jù)線面平行的判定定理可得結論成立．（2）在等腰中梯形中，取的中點，連，，證得四邊形為菱形，進而得．同理四邊形為菱形，可得．再由平面平面得到平面，于是得，最后根據(jù)線面垂直的判定可得平面．

證明：（1）如圖，取的中點，連，，

∵為的中點，為的中點，

∴，．

又，，

∴，，

∴四邊形為平行四邊形，

∴．

又平面，平面，

∴平面

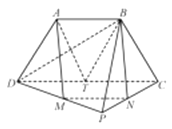
（2）如圖，在等腰中梯形中，取的中點，連，．

∵，，

∴，，

∴四邊形為平行四邊形．

又，

∴四邊形為菱形，

∴．

同理，四邊形為菱形，

∴．

∵，

∴．

∵平面平面，平面平面，，平面，

∴平面，

又平面，

∴．

∵，，

∴平面．