
已知動點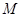 到點
到點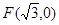 的距離與到直線
的距離與到直線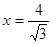 的距離之比為定值
的距離之比為定值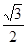 ,記
,記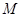 的軌跡為
的軌跡為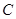 .
.

(1)求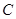 的方程,并畫出
的方程,并畫出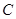 的簡圖;
的簡圖;
(2)點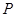 是圓
是圓 上第一象限內的任意一點,過
上第一象限內的任意一點,過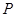 作圓的切線交軌跡
作圓的切線交軌跡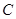 于
于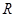 ,
,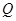 兩點.
兩點.
(i)證明: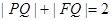 ;
;
(ii)求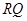 的最大值.
的最大值.
(1)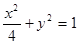 ,C的圖象是橢圓.
,C的圖象是橢圓.
(2)(i)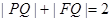 。(ii)當
。(ii)當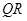 過點
過點 時取最大值2
時取最大值2
【解析】
試題分析:(1)設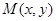 ,由題動點M滿足:
,由題動點M滿足: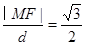 1分
1分

其中: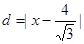 ,
,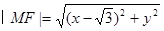
...2分
代入,化簡得: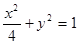
C的圖象是橢圓,如圖所示. 4分
(2)(i)設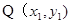 ,
,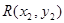
則 5分
5分
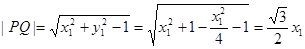 6分
6分
即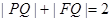 7分
7分
(ii)解法一、設切線為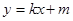 ,由題
,由題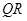 與圓相切,得
與圓相切,得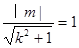 ,
,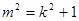
8分
再由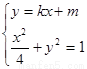 ,得
,得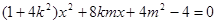 9分
9分
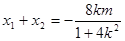 10分
10分
由(i)知 ,所以
,所以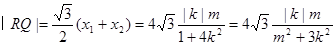
11分
又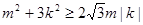 . 2分
. 2分
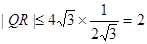 ,當
,當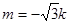 時,取最大值2
13分
時,取最大值2
13分
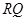 的最大值為2.
...14分
的最大值為2.
...14分
解法二、
由(i)同理得 ,則
,則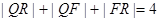
又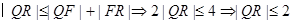
當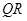 過點
過點 時取最大值2
時取最大值2
考點:本題主要考查橢圓的標準方程,橢圓的幾何性質,直線與圓、直線與橢圓的位置關系,弦長公式。
點評:中檔題,求橢圓的標準方程,主要運用了橢圓的幾何性質,a,b,c,e的關系。曲線關系問題,往往通過聯立方程組,得到一元二次方程,運用韋達定理。涉及弦長問題,一般要利用韋達定理,簡化解題過程。本題“幾何味”較濃,應認真分析幾何特征。


科目:高中數學 來源: 題型:
(14分)已知動點![]() 到點
到點![]() 的距離與到直線
的距離與到直線![]() 的距離之比為
的距離之比為![]() 。
。
(I)求動點![]() 的軌跡C的方程;
的軌跡C的方程;
(Ⅱ)若過點![]() 的直線與曲線
的直線與曲線![]() 在
在![]() 軸左側交于不同的兩點
軸左側交于不同的兩點![]() ,點
,點![]() 滿足
滿足
![]() ,求直線
,求直線![]() 在
在![]() 軸上的截距
軸上的截距![]() 的取值范圍。
的取值范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:
已知動點![]() 到點
到點![]() 的距離與到直線
的距離與到直線![]() 的距離之比為
的距離之比為![]() 。
。
(I)求動點![]() 的軌跡C的方程;(Ⅱ)若過點
的軌跡C的方程;(Ⅱ)若過點![]() 的直線與曲線
的直線與曲線![]() 在
在![]() 軸左側交于不同的兩點
軸左側交于不同的兩點![]() ,點
,點![]() 滿足
滿足 ![]() ,求直線
,求直線![]() 在
在![]() 軸上的截距
軸上的截距![]() 的取值范圍。
的取值范圍。
查看答案和解析>>
科目:高中數學 來源:2010-2011學年重慶市高三高考前沖刺試卷文數 題型:解答題
(本小題滿分12分)
已知動點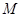 到點
到點
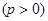 的距離比它到
的距離比它到 軸的距離多
軸的距離多 ·
·
(Ⅰ)求動點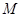 的軌跡方程;
的軌跡方程;
(Ⅱ)設動點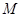 的軌跡為
的軌跡為 ,過點
,過點 的直線
的直線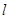 與曲線
與曲線 交于
交于 兩點,若
兩點,若 軸正半軸上存在點
軸正半軸上存在點 使得
使得 是以
是以 為直角頂點的等腰直角三角形,求直線
為直角頂點的等腰直角三角形,求直線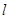 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源:2011屆重慶市高三高考前沖刺試卷文數 題型:解答題
(本小題滿分12分)
已知動點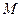 到點
到點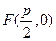
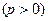 的距離比它到
的距離比它到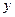 軸的距離多
軸的距離多 ·
·
(Ⅰ)求動點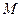 的軌跡方程;
的軌跡方程;
(Ⅱ)設動點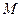 的軌跡為
的軌跡為 ,過點
,過點 的直線
的直線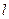 與曲線
與曲線 交于
交于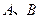 兩點,若
兩點,若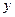 軸正半軸上存在點
軸正半軸上存在點 使得
使得 是以
是以 為直角頂點的等腰直角三角形,求直線
為直角頂點的等腰直角三角形,求直線
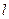 的方程.
的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com