
【題目】已知函數![]() ,
,![]() ,記
,記![]()
(1)證明:![]() 有且僅有一個零點;
有且僅有一個零點;
(2)記![]() 的零點為
的零點為![]() ,
,![]() ,若
,若![]() 在
在![]() 內有兩個不等實根
內有兩個不等實根![]() ,判斷
,判斷![]() 與
與![]() 的大小,并給出對應的證明.
的大小,并給出對應的證明.
【答案】(1)見證明;(2)![]() ,證明見解析
,證明見解析
【解析】
(1)![]() 的零點個數
的零點個數![]() 的零點個數,故只需求
的零點個數,故只需求![]() 的單調性,并利用零點存在性定理得到
的單調性,并利用零點存在性定理得到![]() 有且僅有唯一零點,從而得證;
有且僅有唯一零點,從而得證;
(2)本題實質是極點偏移,先根據(1)和題設得到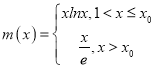 ,再確定
,再確定![]() ,
,![]() ,然后用分析法給出證明,要證:
,然后用分析法給出證明,要證:![]() ,即證
,即證![]() ,而
,而![]() 在
在![]() 上遞減,故可證:
上遞減,故可證:![]() ,又
,又![]() ,故即證
,故即證![]() ,即證
,即證![]() ,接著構造函數
,接著構造函數![]() ,證明其單調性,從而得到結果.
,證明其單調性,從而得到結果.
(1)證明:![]() 的零點個數
的零點個數![]() 的零點個數,
的零點個數,
故要證明![]() 有且僅有一個零點,即證明
有且僅有一個零點,即證明![]() 有且僅有一個零點.
有且僅有一個零點.
∵![]() ,即
,即![]() 在
在![]() 上單增,
上單增,
又![]() ,
,![]() ,
,
由零點存在性定理知:![]() 在
在![]() 上有且僅有唯一零點,
上有且僅有唯一零點,
即![]() 在
在![]() 上有且僅有一個零點;
上有且僅有一個零點;
(2)![]() ,當
,當![]() 時,
時,![]() ,
,
由(1)知存在![]() 使
使![]() ,
,
故![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ,
,
因而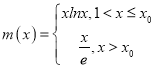 .
.
顯然當![]() 時,
時,![]() ,
,![]() 因而在
因而在![]() 上單增;
上單增;
當![]() 時,
時,![]() ,
,![]() .
.
因而![]() 在
在![]() 上遞減;
上遞減;
若![]() 在
在![]() 有兩個不等實根
有兩個不等實根![]() ,
,![]() ,則
,則![]() ,
,![]() ,
,
顯然當![]() 時,
時,![]() ,
,
而用分析法給出證明,要證:![]() ,即證
,即證![]() ,
,
而![]() 在
在![]() 上遞減,故可證:
上遞減,故可證:
![]() ,又
,又![]() ,
,
故即證![]() ,即證
,即證![]() .
.
記![]() ,則
,則![]() ,
,
故即證![]() ,而
,而![]() ,記
,記![]() ,
,
則![]()
![]() ,
,![]() ,
,
當![]() 時,
時,![]() ;
;![]() 時,
時,![]() ,
,
故![]() ,
,
故當![]() 時,
時,![]() ,
,
故![]() 在
在![]() 上單增,從而當
上單增,從而當![]() 時,
時,![]() ,
,
故![]() 得證.
得證.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】我國南宋數學家楊輝在所著的《詳解九章算法》一書中用如圖所示的三角形解釋二項展開式的系數規律,現把楊輝三角中的數從上到下,從左到右依次排列,得數列:1,1,1,1,2,1,1,3,3,1,1,4,6,4,1,…,記作數列![]() ,若數列
,若數列![]() 的前
的前![]() 項和為
項和為![]() ,則
,則![]() _____.
_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
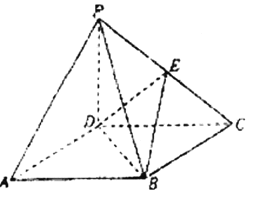
【題目】如圖,四棱錐![]() 的底面
的底面![]() 是正方形,側棱
是正方形,側棱![]() 底面
底面![]() ,
,![]() ,
,![]() 是
是![]() 的中點.
的中點.
(1)證明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)若點![]() 在線段
在線段![]() (不包含端點)上,且直線
(不包含端點)上,且直線![]() 平面
平面![]() ,求線段
,求線段![]() 的長.
的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,射線![]() 的普通方程為
的普通方程為![]() ,曲線
,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).以O為極點,x軸的正半軸為極軸建立極坐標系,曲線
為參數).以O為極點,x軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)寫出![]() 與
與![]() 的極坐標方程;
的極坐標方程;
(2)設![]() 與
與![]() 的交點為P(點P不為極點),
的交點為P(點P不為極點),![]() 與
與![]() 的交點為Q,當
的交點為Q,當![]() 在
在![]() 上變化時,求
上變化時,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】今年入夏以來,我市天氣反復,降雨頻繁.在下圖中統計了上個月前15天的氣溫,以及相對去年同期的氣溫差(今年氣溫-去年氣溫,單位:攝氏度),以下判斷錯誤的是()
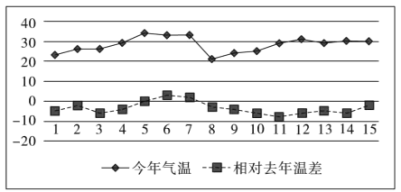
A.今年每天氣溫都比去年氣溫高B.今年的氣溫的平均值比去年低
C.去年8-11號氣溫持續上升D.今年8號氣溫最低
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列結論:
①“![]() 且
且![]() 為真”是“
為真”是“![]() 或
或![]() 為真”的充分不必要條件:②“
為真”的充分不必要條件:②“![]() 且
且![]() 為假”是“
為假”是“![]() 或
或![]() 為真”的充分不必要條件;③“
為真”的充分不必要條件;③“![]() 或
或![]() 為真”是“非
為真”是“非![]() 為假”的必要不充分條件;④“非
為假”的必要不充分條件;④“非![]() 為真”是“
為真”是“![]() 且
且![]() 為假”的必要不充分條件.
為假”的必要不充分條件.
其中,正確的結論是__________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com