【題目】在△
中，角
、
、
所對的邊分別為
、
、
，給出四個命題：
（1）若
，則△為等腰三角形；
（2）若
，則△為直角三角形；
（3）若
，則△為等腰直角三角形；
（4）若
，則△為正三角形；
以上正確命題的個數是（ ）
A. 1 B. 2 C. 3 D. 4
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】己知函數
.
（1）當
時，求函數
的圖象在
處的切線方程；
（2）求函數的單調區間；
（3）是否存在整數
使得函數的極大值大于零，若存在，求的最小整數值，若不存在，說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知拋物線
上的點
到焦點
的距離為
．
（1）求
，
的值；
（2）設
，
是拋物線上分別位于
軸兩側的兩個動點，且
，其中
為坐標原點．求證：直線
過定點，并求出該定點的坐標．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下面幾種推理是類比推理的（ ）
A. 兩條直線平行，同旁內角互補，如果
和
是兩條平行直線的同旁內角，則
B. 由平面三角形的性質，推測空間四邊形的性質
C. 某校高二級有20個班，1班有51位團員，2班有53位團員，3班有52位團員，由此可以推測各班都超過50位團員.
D. 一切偶數都能被2整除，
是偶數，所以能被2整除.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】定義區間
、
、
、
的長度均為
，已知不等式
的解集為
.
（1）求的長度；
（2）函數
（
，
）的定義域與值域都是（
），求區間的最大長度；
（3）關于
的不等式
的解集為
，若
的長度為6，求實數
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
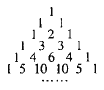
【題目】我國南宋數學家楊輝1261年所著的《詳解九章算法》一書里出現了如圖所示的表，即楊輝三角，這是數學史上的一個偉大成就，在“楊輝三角”中，第
行的所有數字之和為
，若去除所有為1的項，依次構成數列2，3，3，4，6，4，5，10，10，5，…，則此數列的前15項和為（ ）
A. 110B. 114C. 124D. 125
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某省從2021年開始將全面推行新高考制度，新高考“
”中的“2”要求考生從政治、化學、生物、地理四門中選兩科，按照等級賦分計入高考成績，等級賦分規則如下：從2021年夏季高考開始，高考政治、化學、生物、地理四門等級考試科目的考生原始成績從高到低劃分為
五個等級，確定各等級人數所占比例分別為
，
，，
，
，等級考試科目成績計入考生總成績時，將
至
等級內的考生原始成績，依照等比例轉換法分別轉換到
、
、
、
、
五個分數區間，得到考生的等級分，等級轉換分滿分為100分.具體轉換分數區間如下表：
等級 |
|
|
|
|
|
比例 |
|
|
|
|
|
賦分區間 |
|
|
|
|
|
而等比例轉換法是通過公式計算：
其中
，
分別表示原始分區間的最低分和最高分，
、
分別表示等級分區間的最低分和最高分，
表示原始分，
表示轉換分，當原始分為，時，等級分分別為、
假設小南的化學考試成績信息如下表：
考生科目 | 考試成績 | 成績等級 | 原始分區間 | 等級分區間 |
化學 | 75分 |
|
|
|
設小南轉換后的等級成績為，根據公式得：
，
所以
（四舍五入取整），小南最終化學成績為77分.
已知某年級學生有100人選了化學，以半期考試成績為原始成績轉換本年級的化學等級成績，其中化學成績獲得等級的學生原始成績統計如下表：
成績 | 95 | 93 | 91 | 90 | 88 | 87 | 85 |
人數 | 1 | 2 | 3 | 2 | 3 | 2 | 2 |
（1）從化學成績獲得等級的學生中任取2名，求恰好有1名同學的等級成績不小于96分的概率；
（2）從化學成績獲得等級的學生中任取5名，設5名學生中等級成績不小于96分人數為
，求的分布列和期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】每年的金秋十月，越野e族阿拉善英雄會在內蒙古自治區阿拉善盟阿左旗騰格里沙漠舉行，該項目已打造成集沙漠競技運動、汽車文化極致體驗、主題休閑度假為一體的超級汽車文化賽事娛樂綜合體.為了減少對環境的污染，某環保部門租用了特制環保車清潔現場垃圾.通過查閱近5年英雄會參會人數
（萬人）與沙漠中所需環保車輛數量
（輛），得到如下統計表：
參會人數 | 11 | 9 | 8 | 10 | 12 |
所需環保車輛 | 28 | 23 | 20 | 25 | 29 |
（1）根據統計表所給5組數據，求出關于的線性回歸方程
．
（2）已知租用的環保車平均每輛的費用
（元）與數量
（輛）的關系為
.主辦方根據實際參會人數為所需要投入使用的環保車，
每輛支付費用6000元，超出實際需要的車輛，主辦方不支付任何費用.預計本次英雄會大約有14萬人參加，根據（Ⅰ）中求出的線性回歸方程，預測環保部門在確保清潔任務完成的前提下，應租用多少輛環保車？獲得的利潤
是多少？（注：利潤
主辦方支付費用
租用車輛的費用）．
參考公式：
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
