
【題目】已知函數![]() ,不等式
,不等式![]() 對
對![]() 恒成立.
恒成立.
(1)求函數![]() 的極值和實數
的極值和實數![]() 的值;
的值;
(2)已知函數![]() ,
,![]() ,其中
,其中![]() 為自然對數的底數.若存在
為自然對數的底數.若存在![]() ,使得
,使得![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ,不存在極小值;
,不存在極小值;![]() 。(2)
。(2)![]() 。
。
【解析】
(1)利用導數對![]() 求導,由單調區間求得函數的極值. 對不等式
求導,由單調區間求得函數的極值. 對不等式![]() 兩邊取以
兩邊取以![]() 為底的對數,化簡為
為底的對數,化簡為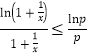 的形式,根據前面所求的單調區間求得
的形式,根據前面所求的單調區間求得![]() 的值.(2)將
的值.(2)將![]() 表達式代入不等式左邊,構造函數
表達式代入不等式左邊,構造函數![]() ,對
,對![]() 分成
分成![]() ,兩類,通過函數的導數,討論函數的單調性,利用函數的最小值為負數,求得
,兩類,通過函數的導數,討論函數的單調性,利用函數的最小值為負數,求得![]() 的取值范圍.
的取值范圍.
(1)![]() ,則
,則![]() 時,
時,![]() ,
,![]() 時,
時,![]() ,
,
故![]() 在區間
在區間![]() 上單調遞增,在
上單調遞增,在![]() 區間上單調遞減,
區間上單調遞減,
故![]() ,不存在極小值.
,不存在極小值.
顯然,![]() 不合題意.
不合題意.
當![]() 時,由
時,由![]() 得
得![]() ,
,
則有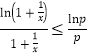 ,
,
故依題意知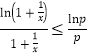 對
對![]() 恒成立.
恒成立.
當![]() 時,
時,![]() 取得最大值
取得最大值![]() ,故
,故![]() .
.
當![]() 時,
時,![]() 取得最大值
取得最大值![]() ,故
,故![]() ,故
,故![]() .
.
綜上得![]() .
.
(2)設![]() ,
,
則![]() .
.
①當![]() 時,
時,![]() ,
,![]() ,
,![]() ,
,
所以不存在![]() 使得
使得![]() 成立.故
成立.故![]() 不合題意.
不合題意.
②當![]() 時,
時,![]()
![]() ,
,
因![]() 為,所以
為,所以![]() ,
,![]() ,所以
,所以![]() 在
在![]() 恒成立,
恒成立,
故![]() 在
在![]() 上單調遞減,
上單調遞減,![]()
![]() ,
,
則依題意有![]() ,
,
解之得![]() ,
,
故![]() 的取值范圍為
的取值范圍為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】經觀測,某公路段在某時段內的車流量![]() (千輛/小時)與汽車的平均速度
(千輛/小時)與汽車的平均速度![]() (千米/小時)之間有函數關系:
(千米/小時)之間有函數關系:![]() .
.
(1)在該時段內,當汽車的平均速度![]() 為多少時車流量
為多少時車流量![]() 最大?最大車流量為多少?(精確到0.01)
最大?最大車流量為多少?(精確到0.01)
(2)為保證在該時段內車流量至少為10千輛/小時,則汽車的平均速度應控制在什么范圍內?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】根據某電子商務平臺的調查統計顯示,參與調查的1 000位上網購物者的年齡情況如圖所示.
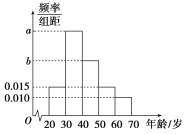
(1)已知[30,40),[40,50),[50,60)三個年齡段的上網購物者人數成等差數列,求![]() 的值;
的值;
(2)該電子商務平臺將年齡在[30,50)內的人群定義為高消費人群,其他年齡段的人群定義為潛在消費人群,為了鼓勵潛在消費人群的消費,該平臺決定發放代金券,高消費人群每人發放50元的代金券,潛在消費人群每人發放100元的代金券,現采用分層抽樣的方式從參與調查的1 000位上網購物者中抽取10人,并在這10人中隨機抽取3人進行回訪,求此3人獲得代金券總和![]() (單位:元)的分布列與數學期望.
(單位:元)的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4,極坐標與參數方程
已知在平面直角坐標系![]() 中,
中,![]() 為坐標原點,曲線
為坐標原點,曲線![]() (
(![]() 為參數),在以平面直角坐標系的原點為極點,
為參數),在以平面直角坐標系的原點為極點,![]() 軸的正半軸為極軸,取相同單位長度的極坐標系中,直線
軸的正半軸為極軸,取相同單位長度的極坐標系中,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的普通方程和直線
的普通方程和直線![]() 的直角坐標方程;
的直角坐標方程;
(2)直線![]() 與
與![]() 軸的交點
軸的交點![]() ,經過點
,經過點![]() 的直線
的直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,若
兩點,若![]() ,求直線
,求直線![]() 的傾斜角.
的傾斜角.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一臺還可以用的機器由于使用的時間較長,它按不同的轉速生產出來的某機械零件有一些會有缺陷,每小時生產有缺陷零件的多少隨機器運轉的速率而變化,下表為抽樣試驗結果:
轉速x(轉/秒) | 16 | 14 | 12 | 8 |
每小時生產有缺陷的零件數y(件) | 11 | 9 | 8 | 5 |
(1)畫出散點圖;
(2)如果y與x有線性相關的關系,求回歸直線方程;
(3)若實際生產中,允許每小時生產的產品中有缺陷的零件最多為10個,那么機器的運轉速度應控制在什么范圍內?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】圖1是由矩形![]() 和菱形
和菱形![]() 組成的一個平面圖形,其中
組成的一個平面圖形,其中![]() ,
, ![]() ,將其沿
,將其沿![]() 折起使得
折起使得![]() 與
與![]() 重合,連結
重合,連結![]() ,如圖2.
,如圖2.
(1)證明圖2中的![]() 四點共面,且平面
四點共面,且平面![]() 平面
平面![]() ;
;
(2)求圖2中的四邊形![]() 的面積.
的面積.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com