
(本小題12分)已知數列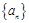 是各項均不為
是各項均不為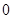 的等差數列,公差為
的等差數列,公差為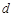 ,
,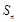 為其前
為其前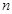 項和,且滿足
項和,且滿足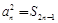 ,
,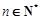 .數列
.數列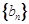 滿足
滿足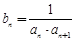 ,
,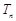 為數列
為數列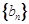 的前n項和.
的前n項和.
(Ⅰ)求數列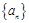 的通項公式
的通項公式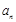 和數列
和數列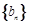 的前n項和
的前n項和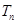 ;
;
(Ⅱ)若對任意的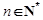 ,不等式
,不等式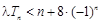 恒成立,求實數
恒成立,求實數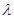 的取值范圍;
的取值范圍;
(1)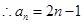 ,
,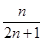 (2)
(2)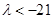
【解析】
試題分析:解(1)在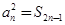 中,令
中,令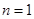 ,
,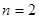 ,
,
得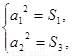 即
即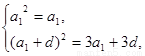
解得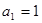 ,
,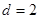 ,
,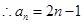
又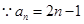 時,
時,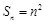 滿足
滿足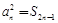 ,
,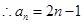 ………………3分
………………3分
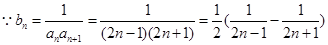 ,
,
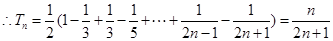 . ………………6分
. ………………6分
(2)①當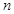 為偶數時,要使不等式
為偶數時,要使不等式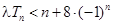 恒成立,即需不等式
恒成立,即需不等式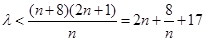 恒成立.
恒成立.
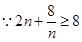 ,等號在
,等號在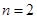 時取得.
時取得.
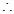 此時
此時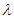 需滿足
需滿足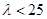 . …………………………………………8分
. …………………………………………8分
②當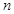 為奇數時,要使不等式
為奇數時,要使不等式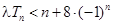 恒成立,即需不等式
恒成立,即需不等式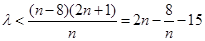 恒成立.
恒成立.
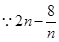 是隨
是隨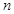 的增大而增大,
的增大而增大, 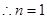 時
時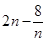 取得最小值
取得最小值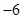 .
.
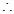 此時
此時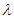 需滿足
需滿足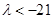 . …………………………………………11分
. …………………………………………11分
綜合①、②可得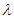 的取值范圍是
的取值范圍是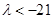 . ………………………………………12分
. ………………………………………12分
考點:本試題考查了數列的通項公式和數列求和求解。
點評:對于等差數列求解通項公式,主要求解兩個基本元素,首項和公差即可。同時對于數列的求和中裂項求和要給予關注,高考常考查,而對于數列與不等式恒成立結合的問題,通常情況下,采用分離的思想來得到范圍,屬于難度試題。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
(本小題12分)已知![]() ,
,![]() ,直線
,直線![]() 與函數
與函數![]() 、
、![]() 的k*s#5^u圖象都相切,且與函數
的k*s#5^u圖象都相切,且與函數![]() 的k*s#5^u圖象的k*s#5^u切點的k*s#5^u橫坐標為
的k*s#5^u圖象的k*s#5^u切點的k*s#5^u橫坐標為![]() .
.
(Ⅰ)求直線![]() 的k*s#5^u方程及
的k*s#5^u方程及![]() 的k*s#5^u值;
的k*s#5^u值;
(Ⅱ)若![]() (其中
(其中![]() 是
是![]() 的k*s#5^u導函數),求函數
的k*s#5^u導函數),求函數![]() 的k*s#5^u最大值;
的k*s#5^u最大值;
(Ⅲ)當![]() 時,求證:
時,求證:![]() .
.
查看答案和解析>>
科目:高中數學 來源:2011年四川省瀘縣二中高2013屆春期重點班第一學月考試數學試題 題型:解答題
(本小題12分)已知等比數列 中,
中, 。
。
(1)求數列 的通項公式;
的通項公式;
(2)設等差數列 中,
中, ,求數列
,求數列 的前
的前 項和
項和 .
.
查看答案和解析>>
科目:高中數學 來源:2011云南省潞西市高二上學期期末考試數學試卷 題型:解答題
(本小題12分)
已知頂點在原點,焦點在 軸上的拋物線與直線
軸上的拋物線與直線 交于P、Q兩點,|PQ|=
交于P、Q兩點,|PQ|= ,求拋物線的方程
,求拋物線的方程
查看答案和解析>>
科目:高中數學 來源:2010年浙江省杭州市七校高二上學期期中考試數學文卷 題型:解答題
(本小題12分)
已知圓C: ;
;
(1)若直線 過
過 且與圓C相切,求直線
且與圓C相切,求直線 的方程.
的方程.
(2)是否存在斜率為1直線 ,使直線
,使直線 被圓C截得弦AB,以AB為直徑的圓經過原點O. 若存在,求
被圓C截得弦AB,以AB為直徑的圓經過原點O. 若存在,求
出直線 的方程;若不存在,說明理由.
的方程;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源:2012屆山東省兗州市高二下學期期末考試數學(文) 題型:解答題
(本小題12分)已知函數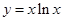
(1) 求這個函數的導數;
(2) 求這個函數的圖像在點 處的切線方程。
處的切線方程。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com