已知函數(shù)
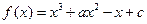
,且
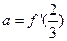
.
(Ⅰ)求
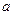
的值;
(Ⅱ)求函數(shù)
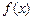
的單調(diào)區(qū)間;
(Ⅲ)設函數(shù)
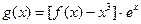
,若函數(shù)
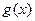
在
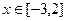
上單調(diào)遞增,求實數(shù)
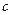
的取值范圍.
解:(Ⅰ)由
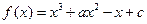
,得
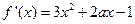
.
當
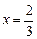
時,得
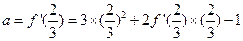
,
解之,得
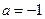
. ……………………4分
(Ⅱ)因為
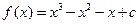
.
從而
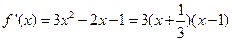
,列表如下:
所以
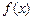
的單調(diào)遞增區(qū)間是
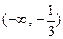
和
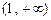
;
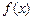
的單調(diào)遞減區(qū)間是
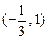
. ……………………9分
(Ⅲ)函數(shù)
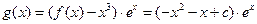
,
有
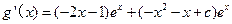
=
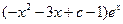
,
因為函數(shù)在區(qū)間
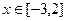
上單調(diào)遞增,
等價于
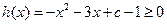
在
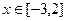
上恒成立,
只要
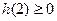
,解得
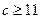
,
所以
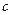
的取值范圍是
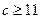
. ……………………14分
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:填空題
半徑為r的圓的面積S(r)=πr2,周長C(r)=2πr,若將r看作(0,+∞)上的變量,則(πr2)′=2πr①,①式可以用語言敘述為:圓的面積函數(shù)的導數(shù)等于圓的周長函數(shù).對于半徑為R的球,若將R看作(0,+∞)上的變量,請你寫出類似于①的式子:_______________________②,②式可以用語言敘述為:________________________.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知函數(shù)f(x)=x3+3ax-1的導函數(shù)f ′ (x),g(x)=f ′(x)-ax-3.
(1)當a=-2時,求函數(shù)f(x)的單調(diào)區(qū)間;
(2)若對滿足-1≤a≤1的一切a的值,都有g(x)<0,求實數(shù)x的取值范圍;
(3)若x·g ′(x)+lnx>0對一切x≥2恒成立,求實數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題満分15分)
已知
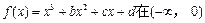
上是增函數(shù),在[0,2]上是減函數(shù),且方程

有三

個根,它們分別為
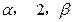
.
(1)求c的值;
(2)求證
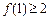
;
(3)求
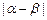
的取值范圍
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知函數(shù)
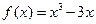
(Ⅰ)求曲線在
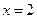
處的切線方程;
(Ⅱ)過點
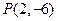
作曲線
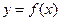
的切線,求此切線的方程.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分12分)如題(21)圖,已知
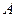
、
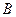
為橢圓
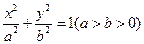
和雙曲線
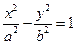
的公共頂點,
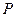
、
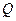
分別為雙曲線和橢圓上不同于
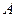
、
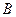
的動點,且
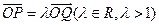
.設
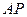
、
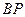
、
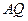
、
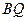
的斜率分別為
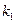
、
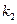
、
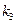
、
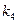
.
(I)求證:
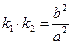
;
(II)求
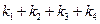
的值;
(III)設
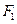
、

分別為雙曲線和橢圓的右焦點,若
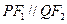
,求
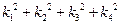
的值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
.若函數(shù)
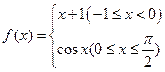
的圖像與
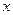
軸圍成的封閉圖形的面積為
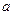
,則
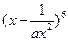
的展開式中的常數(shù)項為( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
函數(shù)
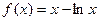
的最小值為
查看答案和解析>>

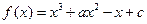 ,且
,且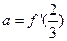 .
.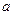 的值;
的值;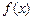 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;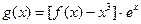 ,若函數(shù)
,若函數(shù)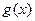 在
在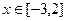 上單調(diào)遞增,求實數(shù)
上單調(diào)遞增,求實數(shù)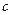 的取值范圍.
的取值范圍. 導學全程練創(chuàng)優(yōu)訓練系列答案
導學全程練創(chuàng)優(yōu)訓練系列答案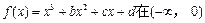 上是增函數(shù),在[0,2]上是減函數(shù),且方程
上是增函數(shù),在[0,2]上是減函數(shù),且方程 有三
有三 個根,它們分別為
個根,它們分別為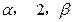 .
.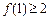 ;
;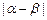 的取值范圍
的取值范圍 、
、 為橢圓
為橢圓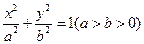 和雙曲線
和雙曲線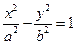 的公共頂點,
的公共頂點, 、
、 分別為雙曲線和橢圓上不同于
分別為雙曲線和橢圓上不同于 、
、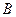 的動點,且
的動點,且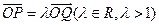 .設
.設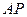 、
、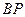 、
、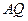 、
、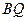 的斜率分別為
的斜率分別為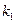 、
、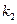 、
、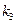 、
、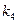 .
.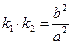 ;
;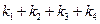 的值;
的值;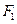 、
、 分別為雙曲線和橢圓的右焦點,若
分別為雙曲線和橢圓的右焦點,若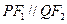 ,求
,求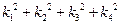 的值.
的值.