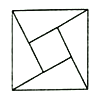
【題目】2002年在北京召開的國際數(shù)學家大會的會標是以我國古代數(shù)學家的弦圖為基礎設計的.弦圖是由四個全等的直角三角形與一個小正方形拼成的一個大正方形（如圖）.設其中直角三角形中較小的銳角為
，且
，如果在弦圖內隨機拋擲1000米黑芝麻（大小差別忽略不計），則落在小正方形內的黑芝麻數(shù)大約為（ ）
A. 350B. 300C. 250D. 200
挑戰(zhàn)100單元檢測試卷系列答案科目：高中數(shù)學 來源： 題型：
【題目】已知橢圓
與直線
交于
兩點，不與
軸垂直，圓
.
（1）若點
在橢圓
上，點
在圓
上，求
的最大值；
（2）若過線段
的中點
且垂直于的直線
過點
，求直線的斜率的取值范圍.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】從盛滿2升純酒精的容器里倒出1升純酒精,然后填滿水,再倒出1升混合溶液后又用水填滿,以此繼續(xù)下去,則至少應倒 次后才能使純酒精體積與總溶液的體積之比低于10%.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】在如圖所示的幾何體中，四邊形
是菱形，
是矩形，平面
平面，
，
，
，
為
的中點．
（1）求證：
∥平面
；
（2）在線段
上是否存在點
，使二面角
的大小為
？若存在，求出
的長；若不存在，請說明理由．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知橢圓
：
的左、右焦點分別為
、
，過的直線
與橢圓相交于
、
兩點．
（1）求
的周長；
（2）設點
為橢圓的上頂點，點在第一象限，點
在線段
上．若
，求點的橫坐標；
（3）設直線不平行于坐標軸，點
為點關于
軸的對稱點，直線
與軸交于點
．求
面積的最大值．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知在平面直角坐標系
中，動點
與兩定點
連線的斜率之積為
，記點的軌跡為曲線
.
（1）求曲線的方程；
（2）若過點
的直線
與曲線交于
兩點，曲線上是否存在點
使得四邊形
為平行四邊形？若存在，求直線的方程，若不存在，說明理由.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】如圖，在正方體
中，點
是線段
上的動點，則下列說法錯誤的是（ ）
A. 當點移動至中點時，直線
與平面
所成角最大且為
B. 無論點在上怎么移動，都有
C. 當點移動至中點時，才有與
相交于一點，記為點
，且
D. 無論點在上怎么移動，異面直線與
所成角都不可能是
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知雙曲線
的兩個焦點為
，
，并且經(jīng)過點
.
（1）求雙曲線的方程；
（2）過點
的直線
與雙曲線有且僅有一個公共點，求直線的方程.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知拋物線
：
上橫坐標為4的點到焦點的距離為5.
（1）求拋物線的方程；
（2）設直線
與拋物線交于兩點
、
，且
，
是弦
中點，過作平行于
軸的直線交拋物線于點
，得到
，再分別過弦
、
的中點作平行于軸的直線依次交拋物線于點
、
，得到
和
，按此方法繼續(xù)下去，解決下列問題：
①求證：
；
②計算的面積
；
③根據(jù)的面積的計算結果，寫出、的面積，請設計一種求拋物線與線段所圍成封閉圖形面積的方法，并求此封閉圖形的面積.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
