
【題目】設數列{an}的前n項和為Sn , 已知a1=1, ![]() ,n∈N* .
,n∈N* .
(1)求a2的值;
(2)求數列{an}的通項公式;
(3)證明:對一切正整數n,有 ![]() .
.
科目:高中數學 來源: 題型:
【題目】某校為了解高一期末數學考試的情況,從高一的所有學生數學試卷中隨機抽取n份試卷進行成績分析,得到數學成績頻率分布直方圖(如圖所示),其中成績在[50,60)的學生人數為6. 
(Ⅰ)估計所抽取的數學成績的眾數;
(Ⅱ)用分層抽樣的方法在成績為[80,90)和[90,100]這兩組中共抽取5個學生,并從這5個學生中任取2人進行點評,求分數在[90,100]恰有1人的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的部分圖象如圖所示,下列說法正確的是( )
)的部分圖象如圖所示,下列說法正確的是( ) 
A.函數f(x)的圖象關于直線x=﹣ ![]() 對稱
對稱
B.函數f(x)的圖象關于點(﹣ ![]() ,0)對稱
,0)對稱
C.若方程f(x)=m在[﹣ ![]() ,0]上有兩個不相等的實數根,則實數m∈(﹣2,﹣
,0]上有兩個不相等的實數根,則實數m∈(﹣2,﹣ ![]() ]
]
D.將函數f(x)的圖象向左平移 ![]() 個單位可得到一個偶函數
個單位可得到一個偶函數
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設 1=a1≤a2≤…≤a7 , 其中a1 , a3 , a5 , a7 成公比為q的等比數列,a2 , a4 , a6成公差為1的等差數列,則q的最小值是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C:x2+y2+2x+a=0上存在兩點關于直線l:mx+y+1=0對稱. (I)求m的值;
(Ⅱ)直線l與圓C交于A,B兩點, ![]()
![]() =﹣3(O為坐標原點),求圓C的方程.
=﹣3(O為坐標原點),求圓C的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,已知R(x0 , y0)是橢圓 ![]() +
+ ![]() =1上的一點,從原點O向圓R(x﹣x0)2+(y﹣y0)2=12作兩條切線,分別交橢圓于P,Q兩點.
=1上的一點,從原點O向圓R(x﹣x0)2+(y﹣y0)2=12作兩條切線,分別交橢圓于P,Q兩點. 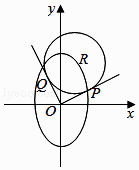
(1)若R點在第一象限,且直線OP,OQ互相垂直,求圓R的方程;
(2)若直線OP,OQ的斜率存在,分別記為k1 , k2 , 求k1k2的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】經過雙曲線 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的右焦點F作該雙曲線一條漸近線的垂線與兩條漸近線相交于M,N兩點,若|MN|=
=1(a>0,b>0)的右焦點F作該雙曲線一條漸近線的垂線與兩條漸近線相交于M,N兩點,若|MN|= ![]() ,則該雙曲線的離心率是( )
,則該雙曲線的離心率是( )
A.2或 ![]()
B.![]() 或
或 ![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓M:x2+(y﹣4)2=4,點P是直線l:x﹣2y=0上的一動點,過點P作圓M的切線PA,PB,切點為A,B.
(1)當切線PA的長度為 ![]() 時,求點P的坐標;
時,求點P的坐標;
(2)若△PAM的外接圓為圓N,試問:當P在直線l上運動時,圓N是否過定點?若存在,求出所有的定點的坐標;若不存在,說明理由.
(3)求線段AB長度的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直角梯形ABCD中,AD∥BC,∠BAD= ![]() ,AB=BC=1,AD=2,E是AD的中點,O是AC與BE的交點,將ABE沿BE折起到A1BE的位置,如圖2. (Ⅰ)證明:CD⊥平面A1OC;
,AB=BC=1,AD=2,E是AD的中點,O是AC與BE的交點,將ABE沿BE折起到A1BE的位置,如圖2. (Ⅰ)證明:CD⊥平面A1OC;
(Ⅱ)若平面A1BE⊥平面BCDE,求平面A1BC與平面A1CD夾角的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com