【題目】已知直線l和平面
，若直線l在空間中任意放置，則在平面內總有直線
和
A.垂直B.平行C.異面D.相交
【答案】A
【解析】
本題可以從直線與平面的位置關系入手：直線與平面的位置關系可以分為三種：直線在平面內、直線與平面相交、直線與平面平行，在這三種情況下再討論平面中的直線與已知直線的關系，通過比較可知：每種情況都有可能垂直．
當直線l與平面
相交時，
平面內的任意一條直線與直線l的關系只有兩種：異面、相交，此時就不可能平行了，故B錯．
當直線l與平面平行時，
平面內的任意一條直線與直線l的關系只有兩種：異面、平行，此時就不可能相交了，故D錯．
當直線a在平面內時，
平面內的任意一條直線與直線l的關系只有兩種：平行、相交，此時就不可能異面了，故C錯．
不管直線l與平面的位置關系相交、平行，還是在平面內，
都可以在平面內找到一條直線與直線
垂直，
因為直線在異面與相交時都包括垂直的情況，故A正確．
故選:A．
科目：高中數學 來源： 題型：
【題目】設圓
的圓心為A，直線l過點B（1,0）且與x軸不重合，l交圓A于C，D兩點，過B作AC的平行線交AD于點E.
（I）證明
為定值，并寫出點E的軌跡方程；
（II）設點E的軌跡為曲線C1，直線l交C1于M,N兩點，過B且與l垂直的直線與圓A交于P,Q兩點，求四邊形MPNQ面積的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，AB為圓O的直徑，點E、F在圓O上，AB
EF，矩形ABCD所在平面和圓O所在平面垂直，已知AB＝2，EF＝1．
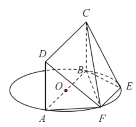
（I）求證：平面DAF⊥平面CBF；
（II）若BC＝1，求四棱錐F－ABCD的體積．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在平面直角坐標系xOy中，已知以M點為圓心的圓
及其上一點
.
（1）設圓N與y軸相切，與圓M外切，且圓心在直線
上，求圓N的標準方程；
（2）設平行于OA的直線l與圓M相交于B，C兩點且
，求直線l的方程.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】2022年北京冬奧會的申辦成功與“3億人上冰雪”口號的提出，將冰雪這個冷項目迅速炒“熱”．北京某綜合大學計劃在一年級開設冰球課程，為了解學生對冰球運動的興趣，隨機從該校一年級學生中抽取了100人進行調查，其中女生中對冰球運動有興趣的占
，而男生有10人表示對冰球運動沒有興趣額．
（1）完成
列聯表，并回答能否有
的把握認為“對冰球是否有興趣與性別有關”？
（2）若將頻率視為概率，現再從該校一年級全體學生中，采用隨機抽樣的方法每次抽取1名學生，抽取5次，記被抽取的5名學生中對冰球有興趣的人數為
，若每次抽取的結果是相互獨立的，求的分布列，期望和方差．
附表：
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
