
(本小題15分)
已知函數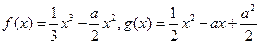 。
。
(I)當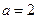 時,求曲線
時,求曲線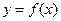 在點
在點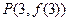 處的切線方程;
處的切線方程;
(Ⅱ)當函數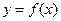 在區間
在區間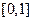 上的最小值為
上的最小值為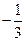 時,求實數
時,求實數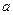 的值;
的值;
(Ⅲ)若函數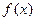 與
與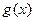 的圖象有三個不同的交點,求實數
的圖象有三個不同的交點,求實數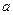 的取值范圍。
的取值范圍。
(I)因為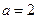 ,由題意
,由題意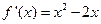 (2分)
(2分) 即過點
即過點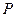 的切線斜率為3,又點
的切線斜率為3,又點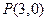
則過點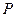 的切線方程為:
的切線方程為: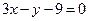 (5分)
(5分)
(Ⅱ)右題意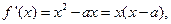 令
令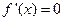 得
得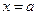 或
或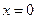 (6分)
(6分)
由 ,要使函數
,要使函數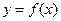 在區間
在區間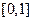 上的最小值為
上的最小值為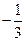 ,則
,則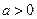
(i)當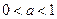 時,
時,
當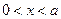 時,
時, ,當
,當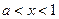 時,
時,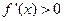 ,
,
所以函數
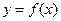 在區間[0,1]上,
在區間[0,1]上,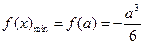
即: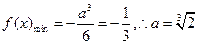 ,舍去 (8分)
,舍去 (8分)
(ii)當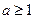 時,
時,
當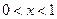 時,
時, ,則使函數
,則使函數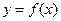 在區間
在區間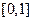 上單調遞減,
上單調遞減,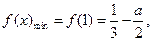
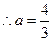
綜上所述: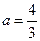 (10分)
(10分)
(Ⅲ)設

令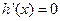 得
得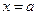 或
或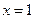 (11分)
(11分)
(i)當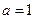 時,函數
時,函數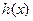 單調遞增,函數
單調遞增,函數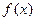 與
與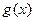 的圖象不可能有三個不同的交點
的圖象不可能有三個不同的交點
(ii)當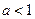 時,
時,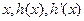 隨
隨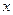 的變化情況如下表:
的變化情況如下表: