
【題目】已知定義在![]() 的奇函數
的奇函數![]() 滿足:①
滿足:①![]() ;②對任意
;②對任意![]() 均有
均有![]() ;③對任意
;③對任意![]() ,均有
,均有![]() .
.
(1)求![]() 的值;
的值;
(2)利用定義法證明![]() 在
在![]() 上單調遞減;
上單調遞減;
(3)若對任意![]() ,恒有
,恒有![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)0(2)見解析(3)![]()
【解析】
(1)用賦值法令![]() ,即可求解;
,即可求解;
(2)根據函數的單調性定義,設![]() ,比較
,比較![]() 大小,做差
大小,做差![]() ,利用條件等式轉化為一個函數值,或對
,利用條件等式轉化為一個函數值,或對![]() 按已知等式賦值將函數值的差轉化為一個函數值,判斷該函數值的正負,即可得出結論;
按已知等式賦值將函數值的差轉化為一個函數值,判斷該函數值的正負,即可得出結論;
(3)根據已知條件求出![]() 或
或![]() ,利用函數的單調性,不等式轉化為對任意
,利用函數的單調性,不等式轉化為對任意![]() ,不等式
,不等式![]() 或者
或者![]() 恒成立,令
恒成立,令![]() ,
,![]() ,則
,則![]() ,
,![]() ,則不等式等價于
,則不等式等價于![]() ……①或
……①或![]() ……②對任意
……②對任意![]() 恒成立,
恒成立,![]() ,
,![]() ,轉化二次函數最值的不等量關系,即可求解.
,轉化二次函數最值的不等量關系,即可求解.
解:(1)在![]() 中,
中,
令![]() ;
;
(2)由題知:對任意![]() 都有
都有![]() ,
,
且對任意![]() 均有
均有![]()
證一:任取![]() ,則
,則
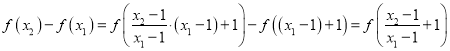 ,
,
因為![]() ,所以
,所以![]() ,
,
所以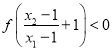 ,
,
即![]() 即
即![]() ,也即
,也即![]() 在
在![]() 單調遞減;
單調遞減;
證二:任取![]() ,設
,設![]() ,
,![]() ,
,![]() ,
,![]() ,
,
則![]() ,
,
因為![]() ,
,![]() 所以
所以![]() ,即
,即![]() ,
,
也即![]() 在
在![]() 單調遞減;
單調遞減;
(3)在![]() 中
中
令![]() ,
,
令![]() ,
,![]() ,
,
而![]() 為奇函數,故
為奇函數,故![]() ,
,
又![]() 在
在![]() 及
及![]() 上均單調遞減,
上均單調遞減,
因此原不等式等價于對任意![]() ,
,
不等式![]() 或者
或者![]() 恒成立,
恒成立,
令![]() ,
,![]() ,則
,則![]() ,
,
![]() ,則不等式等價于
,則不等式等價于
![]() ……①或
……①或![]() ……②
……②
對任意![]() 恒成立,
恒成立,
法一:令![]() ,
,![]() 立,
立,![]() 開口向上,
開口向上,
則不等式①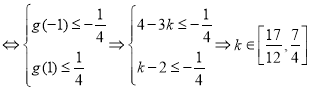 ;
;
對于②,當![]() 時,由
時,由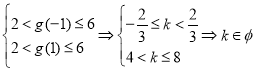 ,
,
即必不存在![]() 滿足②.
滿足②.
綜上,![]() .
.
法二:
令![]() ,
,![]() ,
,
![]() 開口向上,對稱軸為
開口向上,對稱軸為![]() ,
,
且![]() ,
,![]() ,
,![]() ,
,
1°當![]() 即
即![]() 時,問題等價于
時,問題等價于
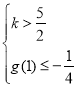 或
或 ,解得
,解得![]() ;
;
2°當![]() 即
即![]() 時,
時,
問題等價于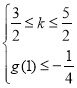 或
或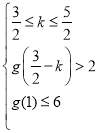 ,
,
解得![]() ;
;
3°當![]() 即
即![]() 時,
時,
問題等價于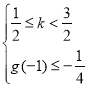 或
或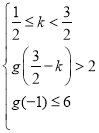 ,
,
解得![]() ;
;
4°當![]() 即
即![]() 時,
時,
問題等價于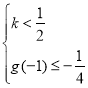 或
或 ,解得
,解得![]() ;
;
綜上,![]()


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】為了解重慶市高中學生在面對新高考模式“3+1+2”的科目選擇中,物理與歷史的二選一是否與性別有關,某高中隨機對該校50名高一學生進行了問卷調查得到相關數據如下列聯表:
選物理 | 選歷史 | 合計 | |
男生 | 5 | ||
女生 | 10 | ||
合計 |
己知在這50人中隨機抽取1人,抽到選物理的人的概率為![]() 。
。
(1)請將上面的列聯表補充完整,并判斷是否有99.5%的把握認為物理與歷史的二選一與性別有關?
| 0.15 | 0.10 | 0.05 | 0.01 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
(參考公式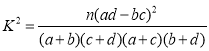 ,其中
,其中![]() 為樣本容量)
為樣本容量)
(2)己知在選物理的10位女生中有3人選擇了化學、地理,有5人選擇了化學、生物,有2人選擇了生物、地理,現從這10人中抽取3人進行更詳細的學科意愿調查,記抽到的3人中選擇化學的有X人,求隨機變量X的分布列及數學期望。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解某養殖產品在某段時間內的生長情況,在該批產品中隨機抽取了120件樣本,測量其增長長度(單位:![]() ),經統計其增長長度均在區間
),經統計其增長長度均在區間![]() 內,將其按
內,將其按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成6組,制成頻率分布直方圖,如圖所示其中增長長度為
分成6組,制成頻率分布直方圖,如圖所示其中增長長度為![]() 及以上的產品為優質產品.
及以上的產品為優質產品.

(1)求圖中![]() 的值;
的值;
(2)已知這120件產品來自于![]() ,B兩個試驗區,部分數據如下列聯表:
,B兩個試驗區,部分數據如下列聯表:

將聯表補充完整,并判斷是否有99.99%的把握認為優質產品與A,B兩個試驗區有關系,并說明理由;
下面的臨界值表僅供參考:

(參考公式: ,其中
,其中![]() )
)
(3)以樣本的頻率代表產品的概率,從這批產品中隨機抽取4件進行分析研究,計算抽取的這4件產品中含優質產品的件數![]() 的分布列和數學期望E(X).
的分布列和數學期望E(X).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 上一點
上一點![]() 到焦點
到焦點![]() 的距離
的距離![]() ,傾斜角為
,傾斜角為![]() 的直線經過焦點
的直線經過焦點![]() ,且與拋物線交于兩點
,且與拋物線交于兩點![]() 、
、![]() .
.
(1)求拋物線的標準方程及準線方程;
(2)若![]() 為銳角,作線段
為銳角,作線段![]() 的中垂線
的中垂線![]() 交
交![]() 軸于點
軸于點![]() .證明:
.證明:![]() 為定值,并求出該定值.
為定值,并求出該定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)求函數![]() 在
在![]() 上的單調遞增區間;
上的單調遞增區間;
(2)將函數![]() 的圖象向左平移
的圖象向左平移![]() 個單位長度,再將圖象上所有點的橫坐標伸長到原來的
個單位長度,再將圖象上所有點的橫坐標伸長到原來的![]() 倍(縱坐標不變),得到函數
倍(縱坐標不變),得到函數![]() 的圖象.求證:存在無窮多個互不相同的整數
的圖象.求證:存在無窮多個互不相同的整數![]() ,使得
,使得![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年9月24日,阿貝爾獎和菲爾茲獎雙料得主、英國著名數學家阿蒂亞爵士宣布自己證明了黎曼猜想,這一事件引起了數學屆的震動。在1859年的時候,德國數學家黎曼向科學院提交了題目為《論小于某值的素數個數》的論文并提出了一個命題,也就是著名的黎曼猜想。在此之前,著名數學家歐拉也曾研究過這個問題,并得到小于數字![]() 的素數個數大約可以表示為
的素數個數大約可以表示為![]() 的結論。若根據歐拉得出的結論,估計1000以內的素數的個數為_________(素數即質數,
的結論。若根據歐拉得出的結論,估計1000以內的素數的個數為_________(素數即質數,![]() ,計算結果取整數)
,計算結果取整數)
A. 768 B. 144 C. 767 D. 145
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=4cosωxsin(ωx![]() )(ω>0)的最小正周期是π.
)(ω>0)的最小正周期是π.
(1)求函數f(x)在區間(0,π)上的單調遞增區間;
(2)若f(x0)![]() ,x0∈[
,x0∈[![]() ,
,![]() ],求cos2x0的值.
],求cos2x0的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com