
(1)當AC、CD、DB滿足怎樣的關系時,△ACP ∽△PDB?
(2)當△ACP ∽△PDB時,求∠APB的度數.
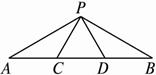
圖1-11
思路分析:本題是一個探索型的問題,考查相似三角形的判定及性質,它給出了一個條件,讓你自己再添加一個條件,可使兩個三角形相似,因此,首先想到相似的判定方法,因又限制了三條邊的關系,所以是對應邊就成比例.當三角形相似了,那么對應角相等,易求∠APB.
解:(1)∵△PCD是等邊三角形,?
∴∠PCD=∠PDC=60°,PD =PC =CD.?
從而∠ACP =∠PDB =120°.?
∴當![]() =
=![]() 時,△ACP∽△PDB,?
時,△ACP∽△PDB,?
即當CD2=AC·BD時,△ACP∽△PDB.?
(2)當△ACP∽△PDB時,∠APB =∠APC+∠CPD +∠DPB?
=∠PBD +60°+∠DPB?
=60°+60°=120°.


 期末好成績系列答案
期末好成績系列答案 99加1領先期末特訓卷系列答案
99加1領先期末特訓卷系列答案 百強名校期末沖刺100分系列答案
百強名校期末沖刺100分系列答案 好成績1加1期末沖刺100分系列答案
好成績1加1期末沖刺100分系列答案 金狀元績優好卷系列答案
金狀元績優好卷系列答案科目:高中數學 來源: 題型:
 如圖,已知點P為橢圓
如圖,已知點P為橢圓| x2 |
| 25 |
| y2 |
| 9 |
查看答案和解析>>
科目:高中數學 來源: 題型:
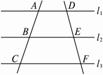
圖1-2-11
A.![]() =
=![]() B.
B.![]() =
=![]() C.
C.![]() =
=![]() D.
D.![]() =
=![]()
查看答案和解析>>
科目:高中數學 來源: 題型:

圖2-11
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源:2012年江蘇省高一上學期開學考試數學 題型:解答題
(本題11分)如圖1,拋物線y=ax2+bx+c(a≠0)的頂點為(1,4),交x軸于A、B,交y軸于D,其中B點的坐標為(3,0)
(1)求拋物線的解析式
(2)如圖2,過點A的直線與拋物線交于點E,交y軸于點F,其中E點的橫坐標為2,若直線PQ為拋物線的對稱軸,點G為PQ上一動點,則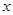 軸上是否存在一點H,使D、G、F、H四點圍成的四邊形周長最小.若存在,求出這個最小值及G、H的坐標;若不存在,請說明理由.
軸上是否存在一點H,使D、G、F、H四點圍成的四邊形周長最小.若存在,求出這個最小值及G、H的坐標;若不存在,請說明理由.
(3)如圖3,拋物線上是否存在一點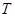 ,過點
,過點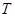 作
作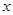 軸的垂線,垂足為
軸的垂線,垂足為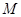 ,過點
,過點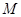 作直線
作直線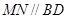 ,交線段
,交線段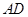 于點
于點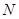 ,連接
,連接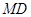 ,使
,使 ~
~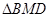 ,若存在,求出點
,若存在,求出點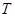 的坐標;若不存在,說明理由.
的坐標;若不存在,說明理由.
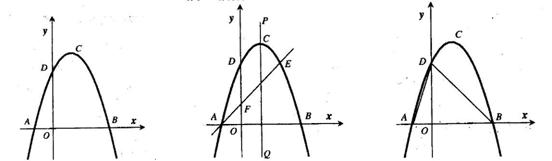 圖1
圖2
圖3
圖1
圖2
圖3
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com