
【題目】已知函數![]() ,
, ![]()
![]() .
.
(I)當a=2時,求曲線y = ![]() 在點(0,f(0))處的切線方程;
在點(0,f(0))處的切線方程;
(II)求函數![]() 在區間[0 , e -1]上的最小值.
在區間[0 , e -1]上的最小值.
【答案】(Ⅰ)![]() ;(Ⅱ)見解析.
;(Ⅱ)見解析.
【解析】試題分析:(1)先根據導數幾何意義得切線斜率為![]() ,再根據點斜式求切線方程(2)先求導數,再根據定義區間分類討論導函數符號變化規律:當
,再根據點斜式求切線方程(2)先求導數,再根據定義區間分類討論導函數符號變化規律:當![]() 時,導數非負,函數為增函數;當
時,導數非負,函數為增函數;當![]() 時,導數非正,函數為減函數;當
時,導數非正,函數為減函數;當![]() 時,導數先負后正,函數先增后減,最后根據單調性確定最小值
時,導數先負后正,函數先增后減,最后根據單調性確定最小值
試題解析:(I)f (x)的定義域為![]() .
.
因為![]() ,a = 2,
,a = 2,
所以![]() ,
, ![]() .
.
所以 函數f (x)在點![]() 處的切線方程是
處的切線方程是 ![]() .
.
(II)由題意可得 ![]() .
.
(1)當![]() 時,
時, ![]() ,
,
所以![]() 在
在![]() 上為減函數,
上為減函數,
所以在區間![]() 上,
上, ![]() .
.
(2) 當![]() 時, 令
時, 令![]() ,則
,則![]() ,
,
① 當![]() ,即
,即![]() 時,
時,
對于![]() ,
, ![]() ,
,
所以f (x)在![]() 上為增函數,
上為增函數,
所以![]() .
.
② 當![]() ,即
,即![]() 時,
時,
對于![]() ,
, ![]() ,
,
所以f (x)在![]() 上為減函數,
上為減函數,
所以![]() .
.
③ 當![]() 即
即![]() 時,
時,
當x變化時, ![]() ,
, ![]() 的變化情況如下表:
的變化情況如下表:
| 0 |
|
|
|
|
| - | 0 | + | ||
|
| 極小值 |
|
所以 ![]() .
.
綜上,
當![]() 時,
時, ![]() ;
;
當![]() 時,
時, ![]() ;
;
當![]() 時,
時, ![]() .
.


 中考解讀考點精練系列答案
中考解讀考點精練系列答案科目:高中數學 來源: 題型:
【題目】甲、乙兩家外賣公司,其送餐員的日工資方案如下:甲公司的底薪70元,每單抽成3元;乙公司無底薪,40單以內(含40單)的部分每單抽成5元,超出40單的部分每單抽成7元,假設同一公司送餐員一天的送餐單數相同,現從兩家公司各隨機抽取一名送餐員,并分別記錄其100天的送餐單數,得到頻數表如下:
甲公司送餐員送餐單數頻數表
送餐單數 | 38 | 39 | 40 | 41 | 42 |
天數 | 20 | 40 | 20 | 10 | 10 |
乙公司送餐員送餐單數頻數表
送餐單數 | 38 | 39 | 40 | 41 | 42 |
天數 | 10 | 20 | 20 | 40 | 10 |
將上表中的頻率視為概率,回答下列問題:
(1)現從甲公司隨機抽取3名送餐員,求恰有2名送餐員送餐單數超過40的概率;
(2)(i)記乙公司送餐員日工資為X(單位:元),求X的數學期望;
(ii)某人擬到甲、乙兩家公司中的一家應聘送餐員,如果僅從日平均工資的角度考慮,他應該選擇去哪家公司應聘,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐PABC中,不能證明AP⊥BC的條件是( )
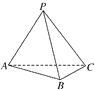
A. AP⊥PB,AP⊥PC
B. AP⊥PB,BC⊥PB
C. 平面BPC⊥平面APC,BC⊥PC
D. AP⊥平面PBC
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著“中華好詩詞”節目的播出,掀起了全民誦讀傳統詩詞經典的熱潮.某大學社團為調查大學生對于“中華詩詞”的喜好,在該校隨機抽取了40名學生,記錄他們每天學習“中華詩詞”的時間,并整理得到如下頻率分布直方圖:
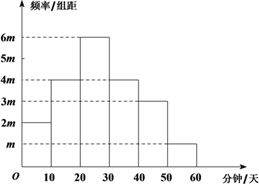
根據學生每天學習“中華詩詞”的時間,可以將學生對于“中華詩詞”的喜好程度分為三個等級 :
學習時間 (分鐘/天) |
|
|
|
等級 | 一般 | 愛好 | 癡迷 |
(Ⅰ) 求![]() 的值;
的值;
(Ⅱ) 從該大學的學生中隨機選出一人,試估計其“愛好”中華詩詞的概率;
(Ⅲ) 假設同組中的每個數據用該組區間的右端點值代替,試估計樣本中40名學生每人每天學習“中華詩詞”的時間.
查看答案和解析>>
科目:高中數學 來源: 題型:
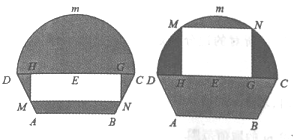
【題目】如圖所示的自動通風設施.該設施的下部![]() 是等腰梯形,其中
是等腰梯形,其中![]() 為2米,梯形的高為1米,
為2米,梯形的高為1米, ![]() 為3米,上部
為3米,上部![]() 是個半圓,固定點
是個半圓,固定點![]() 為
為![]() 的中點.
的中點. ![]() 是由電腦控制可以上下滑動的伸縮橫桿(橫桿面積可忽略不計),且滑動過程中始終保持和
是由電腦控制可以上下滑動的伸縮橫桿(橫桿面積可忽略不計),且滑動過程中始終保持和![]() 平行.當
平行.當![]() 位于
位于![]() 下方和上方時,通風窗的形狀均為矩形
下方和上方時,通風窗的形狀均為矩形![]() (陰影部分均不通風).
(陰影部分均不通風).
(1)設![]() 與
與![]() 之間的距離為
之間的距離為![]() (
(![]() 且
且![]() )米,試將通風窗的通風面積
)米,試將通風窗的通風面積![]() (平方米)表示成關于
(平方米)表示成關于![]() 的函數
的函數![]() ;
;
(2)當![]() 與
與![]() 之間的距離為多少米時,通風窗的通風面積
之間的距離為多少米時,通風窗的通風面積![]() 取得最大值?
取得最大值?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】關于曲線![]()
![]() 給出下列四個命題:
給出下列四個命題:
(1)曲線![]() 有兩條對稱軸,一個對稱中心
有兩條對稱軸,一個對稱中心
(2)曲線![]() 上的點到原點距離的最小值為1
上的點到原點距離的最小值為1
(3)曲線![]() 的長度
的長度![]() 滿足
滿足![]()
(4)曲線![]() 所圍成圖形的面積
所圍成圖形的面積 ![]() 滿足
滿足![]()
上述命題正確的個數是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com