Question

【題目】已知函數(shù)，．

（）當時，證明：為偶函數(shù)；

（）若在上單調(diào)遞增，求實數(shù)的取值范圍；

（）若，求實數(shù)的取值范圍，使在上恒成立．

Answer 1

【答案】（）證明見解析；（）；（）.

【解析】試題分析：（1）當時，的定義域關(guān)于原點對稱，而，說明為偶函數(shù)；（2）在上任取、，且，則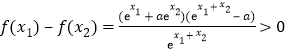恒成立，等價于恒成立，可求得的取值范圍；（3）先證明不等式恒成立，等價于，即恒成立，利用配方法求得的最大值，即可得結(jié)果.

試題解析：（）當時，，定義域關(guān)于原點對稱，

而，說明為偶函數(shù)．

（）在上任取、，且，

則，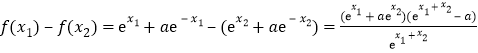

因為，函數(shù)為增函數(shù)，得，，

而在上調(diào)遞增，得，，

于是必須恒成立，

即對任意的恒成立，

∴．

（）由（）、（）知函數(shù)在上遞減，

在上遞增，其最小值，

且，

設(shè)，則，，

于是不等式恒成立，等價于，

即恒成立，

而，僅當，

即時取最大值，故．