
【題目】已知函數(shù)f (x)=ln x+x2-ax(a為常數(shù)).
(1)若x=1是函數(shù)f (x)的一個極值點,求a的值;
(2)當(dāng)0<a≤2時,試判斷f (x)的單調(diào)性;
(3)若對任意的a∈(1,2),x0∈[1,2],不等式f (x0)>mln a 恒成立,求實數(shù)m的取值范圍.
【答案】(1)3;(2)見解析;(3)![]()
【解析】試題分析:(1)求出![]() ,由
,由![]() 列方程即可求
列方程即可求![]() 的值;(2)求出
的值;(2)求出![]() ,在定義域內(nèi),分別令
,在定義域內(nèi),分別令![]() 求得
求得![]() 的范圍,可得函數(shù)
的范圍,可得函數(shù)![]() 增區(qū)間,
增區(qū)間, ![]() 求得
求得![]() 的范圍,可得函數(shù)
的范圍,可得函數(shù)![]() 的減區(qū)間;;(3)問題等價于:對任意的
的減區(qū)間;;(3)問題等價于:對任意的![]() ,不等式
,不等式![]() 恒成立,即
恒成立,即![]() 恒成立,利用導(dǎo)數(shù)研究函數(shù)的單調(diào)性,根單調(diào)性求出
恒成立,利用導(dǎo)數(shù)研究函數(shù)的單調(diào)性,根單調(diào)性求出![]() 的最小值,進而可得結(jié)果.
的最小值,進而可得結(jié)果.
試題解析: f ′(x)=![]() +2x-a.
+2x-a.
(1)由已知得:f ′(1)=0,所以1+2-a=0,所以a=3,經(jīng)驗證符合題意.
(2)當(dāng)0<a≤2時,f ′(x)=![]() +2x-a=
+2x-a=![]()
=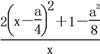 .
.
因為0<a≤2,所以1-![]() >0,而x>0,
>0,而x>0,
即f ′(x)=![]() >0,
>0,
故f (x)在(0,+∞)上是增函數(shù).
(3)當(dāng)a∈(1,2)時,由(2)知,f (x)在[1,2]上的最小值為f (1)=1-a,
故問題等價于:對任意的a∈(1,2),
不等式1-a>mln a恒成立,即m<![]() 恒成立.
恒成立.
記g(a)=![]() (1<a<2),則g′(a)=
(1<a<2),則g′(a)=![]() .
.
令M(a)=-aln a-1+a,則M′(a)=-ln a<0,
所以M(a)在(1,2)上單調(diào)遞減,
所以M(a)<M(1)=0,故g′(a)<0,
所以g(a)=![]() 在a∈(1,2)上單調(diào)遞減,
在a∈(1,2)上單調(diào)遞減,
所以m≤g(2)=![]() =-log2e,
=-log2e,
即實數(shù)m的取值范圍為(-∞,-log2e].


科目:高中數(shù)學(xué) 來源: 題型:
【題目】定義滿足不等式|x![]() A|<B(A∈R,B>0)的實數(shù)x的集合叫做A的B鄰域.若a+b
A|<B(A∈R,B>0)的實數(shù)x的集合叫做A的B鄰域.若a+b![]() t(t為正常數(shù))的a+b鄰域是一個關(guān)于原點對稱的區(qū)間,則a2+b2的最小值為______.
t(t為正常數(shù))的a+b鄰域是一個關(guān)于原點對稱的區(qū)間,則a2+b2的最小值為______.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知定義在R上的函數(shù)f(x)對任意實數(shù)x、y恒有f(x)+f(y)=f(x+y),且當(dāng)x>0時,f(x)<0,又f(1)=-![]() .
.
(1)求證:f(x)為奇函數(shù);
(2)求證:f(x)在R上是減函數(shù);
(3)求f(x)在[-3,6]上的最大值與最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列命題正確的是( )
A. ![]() 是向量
是向量![]() ,
,![]() 不共線的充要條件
不共線的充要條件
B. 在空間四邊形![]() 中,
中,![]()
C. 在棱長為1的正四面體![]() 中,
中,![]()
D. 設(shè)![]() ,
,![]() ,
,![]() 三點不共線,
三點不共線,![]() 為平面
為平面![]() 外一點,若
外一點,若![]() ,則
,則![]() ,
,![]() ,
,![]() ,
,![]() 四點共面
四點共面
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,點![]() 在拋物線
在拋物線![]() 外,過點
外,過點![]() 作拋物線
作拋物線![]() 的兩切線,設(shè)兩切點分別為
的兩切線,設(shè)兩切點分別為![]() ,
,![]() ,記線段
,記線段![]() 的中點為
的中點為![]() .
.

(Ⅰ)求切線![]() ,
,![]() 的方程;
的方程;
(Ⅱ)證明:線段![]() 的中點
的中點![]() 在拋物線
在拋物線![]() 上;
上;
(Ⅲ)設(shè)點![]() 為圓
為圓![]() 上的點,當(dāng)
上的點,當(dāng)![]() 取最大值時,求點
取最大值時,求點![]() 的縱坐標(biāo).
的縱坐標(biāo).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】2016年10月9日,教育部考試中心下發(fā)了《關(guān)于2017年普通高考考試大綱修訂內(nèi)容的通知》,在各科修訂內(nèi)容中明確提出,增加中華優(yōu)秀傳統(tǒng)文化的考核內(nèi)容,積極培育和踐行社會主義核心價值觀,充分發(fā)揮高考命題的育人功能和積極導(dǎo)向作用.宿州市教育部門積極回應(yīng),編輯傳統(tǒng)文化教材,在全市范圍內(nèi)開設(shè)書法課,經(jīng)典誦讀等課程.為了了解市民對開設(shè)傳統(tǒng)文化課的態(tài)度,教育機構(gòu)隨機抽取了200位市民進行了解,發(fā)現(xiàn)支持開展的占![]() ,在抽取的男性市民120人中持支持態(tài)度的為80人.
,在抽取的男性市民120人中持支持態(tài)度的為80人.
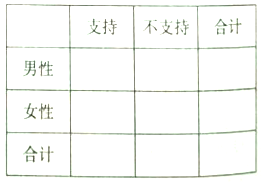
(Ⅰ)完成![]() 列聯(lián)表,并判斷是否有
列聯(lián)表,并判斷是否有![]() 的把握認為性別與支持與否有關(guān)?
的把握認為性別與支持與否有關(guān)?
(Ⅱ)為了進一步征求對開展傳統(tǒng)文化的意見和建議,從抽取的200位市民中對不支持的按照分層抽樣的方法抽取5位市民,并從抽取的5人中再隨機選取2人進行座談,求選取的2人恰好為1男1女的概率.
附: 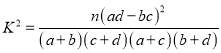 .
.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的離心率為
的離心率為![]() ,其左焦點與拋物線
,其左焦點與拋物線![]() 的焦點重合.
的焦點重合.
(1)求橢圓![]() 的方程;
的方程;
(2)過動點![]() 的直線交
的直線交![]() 軸于點
軸于點![]() ,交橢圓
,交橢圓![]() 于點
于點![]() ,
,![]() 在第一象限,
在第一象限,![]() ,過點
,過點![]() 做
做![]() 軸的垂線交橢圓
軸的垂線交橢圓![]() 于點
于點![]() ,連接
,連接![]() 并延長交橢圓
并延長交橢圓![]() 于另一點
于另一點![]() .設(shè)直線
.設(shè)直線![]() 的斜率分別為
的斜率分別為![]() ,證明:
,證明:![]() 為定值.
為定值.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】汽車的“燃油效率”是指汽車每消耗1升汽油行駛的里程,下圖描述了甲、乙、丙三輛汽車在不同速度下的燃油效率情況. 下列敘述中正確的是( )

A. 消耗1升汽油,乙車最多可行駛5千米
B. 以相同速度行駛相同路程,三輛車中,甲車消耗汽油最多
C. 甲車以80千米/小時的速度行駛1小時,消耗10升汽油
D. 某城市機動車最高限速80千米/小時. 相同條件下,在該市用丙車比用乙車更省油
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() 是定義在[-1,1]上的奇函數(shù),且
是定義在[-1,1]上的奇函數(shù),且![]() ,若任意的
,若任意的![]() ,當(dāng)
,當(dāng)![]() 時,總有
時,總有![]() .
.
(1)判斷函數(shù)![]() 在[-1,1]上的單調(diào)性,并證明你的結(jié)論;
在[-1,1]上的單調(diào)性,并證明你的結(jié)論;
(2)解不等式:![]() ;
;
(3)若![]() 對所有的
對所有的![]() 恒成立,其中
恒成立,其中![]() (
(![]() 是常數(shù)),求實數(shù)
是常數(shù)),求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com