
【題目】給出下列四個命題:
①![]() 中,
中,![]() 是
是![]() 成立的充要條件;
成立的充要條件;
②當![]() 時,有
時,有![]() ;
;
③已知![]() 是等差數列
是等差數列![]() 的前n項和,若
的前n項和,若![]() ,則
,則![]() ;
;
④若函數![]() 為
為![]() 上的奇函數,則函數
上的奇函數,則函數![]() 的圖象一定關于點
的圖象一定關于點![]() 成中心對稱.其中所有正確命題的序號為___________.
成中心對稱.其中所有正確命題的序號為___________.
【答案】①③
【解析】
①利用正弦定理可判斷;②舉反例即可判斷;③利用等差數列等差中項計算可判斷;
④根據奇函數的性質與函數圖象平移可判斷.
①在△ABC中,由正弦定理可得 ![]() , ∴sinA>sinBa>bA>B,因此A>B是sinA>sinB的充要條件,①正確;
, ∴sinA>sinBa>bA>B,因此A>B是sinA>sinB的充要條件,①正確;
②當1>x>0時,lnx<0,所以不一定大于等于2,②不成立;
③等差數列{an}的前n項和,若S7>S5,則S7-S5=a6+a7>0,S9-S3=a4+a5+…+a9=3(a6+a7)>0,因此S9>S3,③正確;
④若函數![]() 為R上的奇函數,則其圖象關于(0,0)中心對稱,而函數y=f(x)的圖象是把y=f(x-
為R上的奇函數,則其圖象關于(0,0)中心對稱,而函數y=f(x)的圖象是把y=f(x-![]() )的圖象向左平移
)的圖象向左平移![]() 個單位得到的,故函數y=f(x)的圖象一定關于點F(-
個單位得到的,故函數y=f(x)的圖象一定關于點F(-![]() ,0)成中心對稱,④不正確.
,0)成中心對稱,④不正確.
綜上只有①③正確.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中數學 來源: 題型:
【題目】(2016·桂林高二檢測)如圖所示,在四邊形ABCD中,AB=AD=CD=1,BD=![]() ,BD⊥CD,將四邊形ABCD沿對角線BD折成四面體A′-BCD,使平面A′BD⊥平面BCD,則下列結論正確的是________.
,BD⊥CD,將四邊形ABCD沿對角線BD折成四面體A′-BCD,使平面A′BD⊥平面BCD,則下列結論正確的是________.

(1)A′C⊥BD.(2)∠BA′C=90°.
(3)CA′與平面A′BD所成的角為30°.
(4)四面體A′-BCD的體積為![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在底面為平行四邊形的四棱錐![]() 中,過點
中,過點![]() 的三條棱PA、AB、AD兩兩垂直且相等,E,F分別是AC,PB的中點.
的三條棱PA、AB、AD兩兩垂直且相等,E,F分別是AC,PB的中點.

(Ⅰ)證明:EF//平面PCD;
(Ⅱ)求EF與平面PAC所成角的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某機構組織語文、數學學科能力競賽,按照一定比例淘汰后,頒發一二三等獎.現有某考場的兩科考試成績數據統計如下圖所示,其中數學科目成績為二等獎的考生有![]() 人.
人.
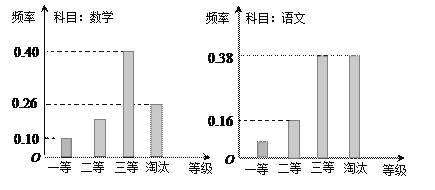

(Ⅰ)求該考場考生中語文成績為一等獎的人數;
(Ⅱ)用隨機抽樣的方法從獲得數學和語文二等獎的學生中各抽取![]() 人,進行綜合素質測試,將他們的綜合得分繪成莖葉圖,求樣本的平均數及方差并進行比較分析;
人,進行綜合素質測試,將他們的綜合得分繪成莖葉圖,求樣本的平均數及方差并進行比較分析;
(Ⅲ)已知本考場的所有考生中,恰有![]() 人兩科成績均為一等獎,在至少一科成績為一等獎的考生中,隨機抽取
人兩科成績均為一等獎,在至少一科成績為一等獎的考生中,隨機抽取![]() 人進行訪談,求兩人兩科成績均為一等獎的概率.
人進行訪談,求兩人兩科成績均為一等獎的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線C:![]() 為參數)和定點
為參數)和定點![]() ,
,![]() ,
,![]() 是曲線C的左,右焦點.
是曲線C的左,右焦點.
(Ⅰ)求經過點![]() 且垂直于直線
且垂直于直線![]() 的直線
的直線![]() 的參數方程;
的參數方程;
(Ⅱ)以坐標原點為極點,![]() 軸的正半軸為極軸建立極坐標系,求直線
軸的正半軸為極軸建立極坐標系,求直線![]() 的極坐標方程.
的極坐標方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com