
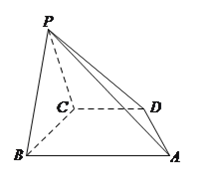
【題目】在四棱錐![]() 中,底面
中,底面![]() 是直角梯形,
是直角梯形, ![]() ,
, ![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() .
.
(Ⅰ)求證: ![]() 平面
平面![]() .
.
(Ⅱ)求平面![]() 和平面
和平面![]() 所成二面角(小于
所成二面角(小于![]() )的大小.
)的大小.
(Ⅲ)在棱![]() 上是否存在點
上是否存在點![]() 使得
使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
【答案】(Ⅰ)見解析(Ⅱ)![]() (Ⅲ)
(Ⅲ)![]() 為
為![]() 的中點,
的中點, ![]()
【解析】試題分析:
(Ⅰ)證明AB⊥平面PBC,利用面面垂直的性質,根據AB⊥BC,平面PBC⊥平面ABCD,即可得證;
(Ⅱ)取BC的中點O,連接PO,證明PO⊥平面ABCD,以O為原點,OB所在的直線為x軸,在平面ABCD內過O垂直于BC的直線為y軸,OP所在的直線為z軸建立空間直角坐標系O-xyz,求出平面PAD的法向量![]() .平面BCP的一個法向量
.平面BCP的一個法向量![]() ,
,
利用向量的夾角公式,即可求得平面ADP和平面BCP所成的二面角;(Ⅲ)在棱PB上存在點M使得CM∥平面PAD,此時![]() ,證明平面MNC∥平面PAD,可得∥平面PAD.
,證明平面MNC∥平面PAD,可得∥平面PAD.
試題解析:
(Ⅰ)∵![]() ,
,
∴![]() ,
,
∵面![]() 面
面![]() ,面
,面![]() 面
面![]() ,
, ![]() 面
面![]() ,
,
∴![]() 面
面![]() .
.
(Ⅱ)取![]() 的中點
的中點![]() ,連接
,連接![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∵面![]() 面
面![]() ,面
,面![]()
![]() ,
, ![]() 面
面![]() ,
,
∴![]() 面
面![]() ,以
,以![]() 為原點,
為原點, ![]() 所在的直線為
所在的直線為![]() 軸,在平面
軸,在平面![]() 內過
內過![]() 且垂直于
且垂直于![]() 的直線為
的直線為![]() 軸,
軸, ![]() 所在的直線為
所在的直線為![]() 軸建立空間直角坐標系
軸建立空間直角坐標系![]() ,如圖所示,
,如圖所示,
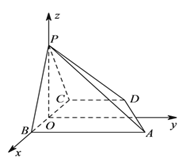
不妨設![]() ,由
,由![]() ,
,
∴![]() ,
, ![]() ,
, ![]() .
.
∴![]() ,
, ![]() .
.
設平面![]() 的法向量為
的法向量為![]() ,
,
∵![]() ,
,
∴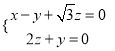 ,
,
令![]() ,則
,則![]() ,
, ![]() .
.
∴![]() .
.
取平面![]() 的一個法向量
的一個法向量![]() ,
,
∴![]() .
.
∴面![]() 和面
和面![]() 的二面角(銳角)的大小為
的二面角(銳角)的大小為![]() .
.
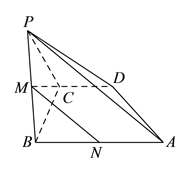
(Ⅲ)在棱![]() 上存在一點
上存在一點![]() 使得
使得![]() 面
面![]() ,此時
,此時![]() .
.
理由如下: ![]() 為
為![]() 的中點,
的中點,
取![]() 的中點
的中點![]() ,連接
,連接![]() ,
, ![]() ,
, ![]() ,
,
則![]() ,
, ![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴四邊形![]() 是平行四邊形.
是平行四邊形.
∴![]() ,
,
∵![]() ,
, ![]() ,
,
∴面![]() 面
面![]() ,
,
∵![]() 面
面![]() ,
,
∴![]() 面
面![]() .
.


科目:高中數學 來源: 題型:
【題目】如圖,P是平行四邊形ABCD所在平面外一點,E是PD的中點. 
(1)求證:PB∥平面EAC;
(2)若M是CD上異于C、D的點.連結PM交CE于G,連結BM交AC于H,求證:GH∥PB.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《最強大腦》是大型科學競技類真人秀節目,是專注傳播腦科學知識和腦力競技的節目.某機構為了了解大學生喜歡《最強大腦》是否與性別有關,對某校的100名大學生進行了問卷調查,得到如下列聯表:
喜歡《最強大腦》 | 不喜歡《最強大腦》 | 合計 | |
男生 | 15 | ||
女生 | 15 | ||
合計 |
已知在這100人中隨機抽取1人抽到不喜歡《最強大腦》的大學生的概率為0.4
( I)請將上述列聯表補充完整;判斷是否有99.9%的把握認為喜歡《最強大腦》與性別有關,并說明理由;
( II)已知在被調查的大學生中有5名是大一學生,其中3名喜歡《最強大腦》,現從這5名大一學生中隨機抽取2人,抽到喜歡《最強大腦》的人數為X,求X的分布列及數學期望.
下面的臨界值表僅參考:
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(參考公式:K2=![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=Asin(ωx+φ),x∈R(其中 ![]() )的圖象與x軸的交點中,相鄰兩個交點之間的距離為
)的圖象與x軸的交點中,相鄰兩個交點之間的距離為 ![]() ,且圖象上一個最低點為
,且圖象上一個最低點為 ![]() . (Ⅰ)求f(x)的解析式;
. (Ⅰ)求f(x)的解析式;
(Ⅱ)當 ![]() ,求f(x)的值域.
,求f(x)的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知直線l1:kx+y=0和直線l2:kx+y+b=0(b>0),射線OC的一個法向量為 ![]() =(﹣k,1),點O為坐標原點,且k≥0,直線l1和l2之間的距離為2,點A、B分別是直線l1、l2上的動點,P(4,2),PM⊥l1于點M,PN⊥OC于點N;
=(﹣k,1),點O為坐標原點,且k≥0,直線l1和l2之間的距離為2,點A、B分別是直線l1、l2上的動點,P(4,2),PM⊥l1于點M,PN⊥OC于點N; 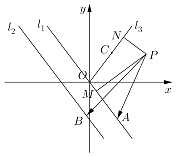
(1)若k=1,求|OM|+|ON|的值;
(2)若| ![]() |=8,求
|=8,求 ![]() 的最大值;
的最大值;
(3)若k=0,AB⊥l2 , 且Q(﹣4,﹣4),試求|PA|+|AB|+|BQ|的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)=2x2+bx+c.
(1)對任意x∈[﹣1,1],f(x)的最大值與最小值之差不大于6,求b的取值范圍;
(2)若f(x)=0有兩個不同實根,f(f(x))無零點,求證: ![]() ﹣
﹣ ![]() >1.
>1.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=Asin(ωx+φ)(A,ω>0,0<|φ|<π)在一個周期內的圖象如圖所示. 
(1)求函數f(x)的解析式;
(2)求g(x)=f(3x+ ![]() )﹣1在[﹣
)﹣1在[﹣ ![]() ,
, ![]() ]上的值域.
]上的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設等比數列{an}的前n項和為Sn , 已知a1=2,且4S1 , 3S2 , 2S3成等差數列.
(Ⅰ)求數列{an}的通項公式;
(Ⅱ)設bn=|2n﹣5|an , 求數列{bn}的前n項和Tn .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com