
【題目】已知函數![]()
![]() .
.
(1)當![]() 時,討論函數
時,討論函數![]() 的單調性;
的單調性;
(2)當![]() ,
, ![]() 時,對任意
時,對任意![]() ,有
,有![]() 成立,求實數
成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)當![]() ,
, ![]() 時,函數
時,函數![]() 在
在![]() 上單調遞增;當
上單調遞增;當![]() ,
, ![]() 時,函數
時,函數![]() 在
在 上單調遞減,在
上單調遞減,在 上單調遞增.(2)
上單調遞增.(2)![]()
【解析】試題分析:(1)求出導數![]() 對
對![]() 分類討論,明確函數函數
分類討論,明確函數函數![]() 的單調性;(2)對任意
的單調性;(2)對任意![]() ,有
,有![]() 成立,等價于
成立,等價于![]() .
. ![]() ,函數
,函數![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增, ![]() 為
為![]() 與
與![]() 中的較大者.
中的較大者.
試題解析:
(1)函數![]() 的定義域為
的定義域為![]() .
.
當![]() 時,
時, ![]() ,所以
,所以![]() .
.
當![]() 時,
時, ![]() ,所以函數
,所以函數![]() 在
在![]() 上單調遞增.
上單調遞增.
當![]() 時,令
時,令![]() ,解得
,解得![]() ,
,
當![]() 時,
時, ![]() ,所以函數
,所以函數![]() 在
在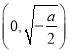 上單調遞減;
上單調遞減;
當![]() 時,
時, ![]() ,所以函數
,所以函數![]() 在
在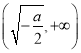 上單調遞增.
上單調遞增.
綜上所述,當![]() ,
, ![]() 時,函數
時,函數![]() 在
在![]() 上單調遞增;
上單調遞增;
當![]() ,
, ![]() 時,函數
時,函數![]() 在
在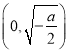 上單調遞減,在
上單調遞減,在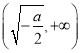 上單調遞增.
上單調遞增.
(2)因為對任意![]() ,有
,有![]() 成立,所以
成立,所以![]() .
.
當![]() 即
即![]() 時,
時, ![]() ,
, ![]() .
.
令![]() ,得
,得![]() ;令
;令![]() ,得
,得![]() .
.
所以函數![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增,
![]() 為
為![]() 與
與![]() 中的較大者.
中的較大者.
設![]()
![]() ,
,
則![]() ,
,
所以![]() 在
在![]() 上單調遞增,故
上單調遞增,故![]() 所以
所以![]() ,
,
從而![]()
![]() .
.
所以![]() 即
即![]() .
.
設![]()
![]() ,則
,則![]() .
.
所以![]() 在
在![]() 上單調遞增.
上單調遞增.
又![]() ,所以
,所以![]() 的解為
的解為![]() .
.
因為![]() ,所以
,所以![]() 的取值范圍為
的取值范圍為![]() .
.


 世紀百通期末金卷系列答案
世紀百通期末金卷系列答案科目:高中數學 來源: 題型:
【題目】某校做了一次關于“感恩父母”的問卷調查,從8~10歲,11~12歲,13~14歲,15~16歲四個年齡段回收的問卷依次為:120份,180份,240份,x份.因調查需要,從回收的問卷中按年齡段分層抽取容量為300的樣本,其中在11~12歲學生問卷中抽取60份,則在15~16歲學生中抽取的問卷份數為( )
A.60 B.80 C.120 D.180
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義在R的函數![]() 是偶函數,且滿足
是偶函數,且滿足![]() 上的解析式為
上的解析式為![]() ,過點
,過點![]() 作斜率為k的直線l,若直線l與函數
作斜率為k的直線l,若直線l與函數![]() 的圖象至少有4個公共點,則實數k的取值范圍是
的圖象至少有4個公共點,則實數k的取值范圍是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
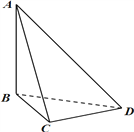
【題目】劉徽(約公元 225 年—295 年)是魏晉時期偉大的數學家,中國古典數學理論的奠基人之一,他的杰作《九章算術注》和《海島算經》是中國寶貴的古代數學遺產. 《九章算術·商功》中有這樣一段話:“斜解立方,得兩壍堵. 斜解壍堵,其一為陽馬,一為鱉臑.” 劉徽注:“此術臑者,背節也,或曰半陽馬,其形有似鱉肘,故以名云.” 其實這里所謂的“鱉臑(biē nào)”,就是在對長方體進行分割時所產生的四個面都為直角三角形的三棱錐. 如圖,在三棱錐![]() 中,
中, ![]() 垂直于平面
垂直于平面![]() ,
, ![]() 垂直于
垂直于![]() ,且
,且 ![]() ,則三棱錐
,則三棱錐![]() 的外接球的球面面積為__________.
的外接球的球面面積為__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2018吉林長春高三下學期二模】為了打好脫貧攻堅戰,某貧困縣農科院針對玉米種植情況進行調研,力爭有效的改良玉米品種,為農民提供技術支.現對已選出的一組玉米的莖高進行統計,獲得莖葉圖如下圖(單位:厘米),設莖高大于或等于180厘米的玉米為高莖玉米,否則為矮莖玉米.
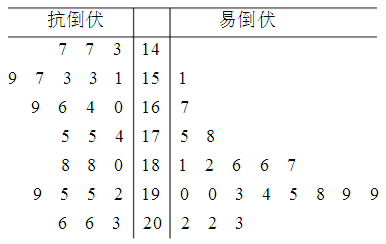
(I)完成列![]() 聯表,并判斷是否可以在犯錯誤的概率不超過1%的前提下,認為抗倒伏與玉米矮莖有關?
聯表,并判斷是否可以在犯錯誤的概率不超過1%的前提下,認為抗倒伏與玉米矮莖有關?
(II)為了改良玉米品種,現采用分層抽樣的方法從抗倒伏的玉米中抽出5株,再從這5株玉米中選取2株進行雜交試驗,選取的植株均為矮莖的概率是多少?

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com