
【題目】已知動圓經過定點![]() ,且與定直線
,且與定直線![]() 相切.
相切.
(1)求動圓圓心![]() 的軌跡方程
的軌跡方程![]() ;
;
(2)已知點![]() ,過點
,過點![]() 作直線
作直線![]() 與
與![]() 交于
交于![]() ,
,![]() 兩點,過點
兩點,過點![]() 作
作![]() 軸的垂線分別與直線
軸的垂線分別與直線![]() ,
,![]() 交于點
交于點![]() ,
,![]() (
(![]() 為原點),求證:
為原點),求證:![]() 為線段
為線段![]() 中點.
中點.
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】雙曲線![]()
![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,過
,過![]() 作傾斜角為
作傾斜角為![]() 的直線與
的直線與![]() 軸和雙曲線的右支分別交于
軸和雙曲線的右支分別交于![]() 兩點,若點
兩點,若點![]() 平分線段
平分線段![]() ,則該雙曲線的離心率是( )
,則該雙曲線的離心率是( )
A. ![]() B.
B. ![]() C. 2 D.
C. 2 D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】變量X與Y相對應的一組數據為(10,1),(11.3,2),(11.8,3),(12.5,4),(13,5);變量U與V相對應的一組數據為(10,5),(11.3,4),(11.8,3),(12.5,2),(13,1).r1表示變量Y與X之間的線性相關系數,r2表示變量V與U之間的線性相關系數,則
A. r2<r1<0 B. r2<0<r1 C. 0<r2<r1 D. r2=r1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知直線
中,已知直線![]() 的參數方程為
的參數方程為 (
(![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,
為極點,![]() 軸的非負半軸為極軸建立極坐標系,曲線
軸的非負半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設點![]() ,直線
,直線![]() 與曲線
與曲線![]() 的交點為
的交點為![]() 、
、![]() ,求
,求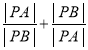 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國著名數學家陳景潤在哥德巴赫猜想的研究中取得了世界矚目的成就,哥德巴赫猜想內容是“每個大于![]() 的偶數可以表示為兩個素數的和”( 注:如果一個大于
的偶數可以表示為兩個素數的和”( 注:如果一個大于![]() 的整數除了
的整數除了![]() 和自身外無其他正因數,則稱這個整數為素數),在不超過
和自身外無其他正因數,則稱這個整數為素數),在不超過![]() 的素數中,隨機選取
的素數中,隨機選取![]() 個不同的素數
個不同的素數![]() 、
、![]() ,則
,則![]() 的概率是( )
的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】煉鋼是一個氧化降碳的過程,由于鋼水含碳量的多少直接影響冶煉時間的長短,因此必須掌握鋼水含碳量和冶煉時間的關系.現已測得爐料熔化完畢時鋼水的含碳量![]() 與冶煉時間
與冶煉時間![]() (從爐料熔化完畢到出鋼的時間)的一組數據,如下表所示:
(從爐料熔化完畢到出鋼的時間)的一組數據,如下表所示:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 104 | 180 | 190 | 177 | 147 | 134 | 150 | 191 | 204 | 121 |
| 100 | 200 | 210 | 185 | 155 | 135 | 170 | 205 | 235 | 125 |
| 10400 | 36000 | 39900 | 32745 | 22785 | 18090 | 25500 | 39155 | 47940 | 15125 |
(1)據統計表明,![]() 與
與![]() 之間具有線性相關關系,請用相關系數
之間具有線性相關關系,請用相關系數![]() 加以說明(
加以說明(![]()
![]() ,則認為
,則認為![]() 與
與![]() 有較強的線性相關關系,否則認為沒有較強的線性相關關系,
有較強的線性相關關系,否則認為沒有較強的線性相關關系,![]() 精確到0.001);
精確到0.001);
(2)建立![]() 關于
關于![]() 的回歸方程(回歸系數的結果精確到0.01);
的回歸方程(回歸系數的結果精確到0.01);
(3)根據(2)中的結論,預測鋼水含碳量為160個0.01%的冶煉時間.
參考公式:回歸方程![]() 中斜率和截距的最小二乘估計分別為
中斜率和截距的最小二乘估計分別為 ,
,
![]() ,相關系數
,相關系數
參考數據: ,
,
![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
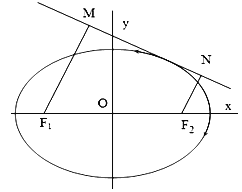
【題目】設點![]() ,
,![]() 分別是橢圓
分別是橢圓![]() 的左、右焦點,
的左、右焦點,![]() 為橢圓
為橢圓![]() 上任意一點,且
上任意一點,且![]() 的最小值為0.
的最小值為0.
(1)求橢圓![]() 的方程;
的方程;
(2)如圖,動直線![]() 與橢圓
與橢圓![]() 有且僅有一個公共點,點
有且僅有一個公共點,點![]() ,
,![]() 是直線
是直線![]() 上的兩點,且
上的兩點,且![]() ,
,![]() ,求四邊形
,求四邊形![]() 面積
面積![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com