
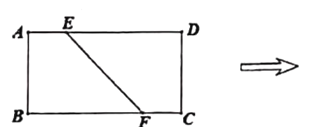
【題目】如圖1,在矩形![]() 中,已知
中,已知![]() ,
,![]() ,點
,點![]() ,
,![]() 分別在邊
分別在邊![]() ,
,![]() 上,且
上,且![]() ,將梯形
,將梯形![]() 沿
沿![]() 折起,使
折起,使![]() 在平面
在平面![]() 上的射影
上的射影![]() 恰好落在線段
恰好落在線段![]() 靠近
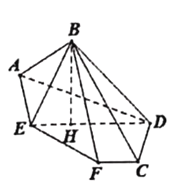
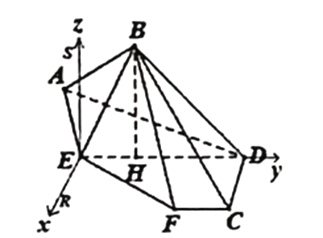
靠近![]() 的三等分點處,得到圖2中的立體圖形.
的三等分點處,得到圖2中的立體圖形.
(1) (2)
(2) 
(1)在圖2中,求證:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的大小.
的大小.
【答案】(1)見解析;(2)![]()
【解析】
(1)根據(jù)![]() 得
得![]() 面
面![]() ,根據(jù)
,根據(jù)![]() 得
得![]() 面
面![]() ,從而得到
,從而得到![]() 面
面![]() ,所以得到所以
,所以得到所以![]() 面
面![]() ;(2)以
;(2)以![]() 為原點建立空間直角坐標系,得到面
為原點建立空間直角坐標系,得到面![]() 的法向量為
的法向量為![]() ,
,![]() 的法向量為
的法向量為![]() ,根據(jù)向量夾角公式得到二面角
,根據(jù)向量夾角公式得到二面角![]() 的大小.
的大小.
(1)證明:在梯形![]() 中,
中,![]() ,
,
而![]() 面
面![]() ,
,![]() 面
面![]() ,
,
所以![]() 面
面![]() ,
,
在梯形![]() 中,
中,![]() ,
,
而![]() 面
面![]() ,
,![]() 面
面![]() ,
,
所以![]() 面
面![]() ,
,
![]() 面
面![]() ,
,![]() ,
,
所以面![]() 面
面![]() ,
,
而![]() 面
面![]() ,
,
所以![]() 面
面![]() ;
;
(2)如圖,過![]() 作
作![]() ,作
,作![]() ,
,
以![]() 為原點,以
為原點,以![]() ,
,![]() ,
,![]() 為
為![]() ,
,![]() ,
,![]() 軸建立空間直角坐標系.
軸建立空間直角坐標系.
由題意可求得![]() ,
,![]() ,所以
,所以![]() ,
,
于是![]() ,又
,又![]() ,
,
所以![]() ,
,![]() ,
,
設(shè)面![]() 的一個法向量為
的一個法向量為![]() ,
,
所以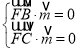 ,則
,則![]()
令![]() ,得
,得![]() ,
,
又知面![]() 的一個法向量為
的一個法向量為![]() ,
,
設(shè)面![]() 與面
與面![]() 所成二面角的大小為
所成二面角的大小為![]() ,易知
,易知![]() 為銳角,
為銳角,
由(1)的證明可知面![]() 平面
平面![]() ,
,
所以二面角![]() ,
,
則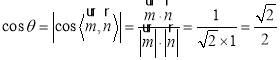 ,
,
即二面角![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】若函數(shù)f(x)=﹣![]() x﹣
x﹣![]() cos2x+m(sinx﹣cosx)在(﹣∞,+∞)上單調(diào)遞減,則m的取值范圍是____________.
cos2x+m(sinx﹣cosx)在(﹣∞,+∞)上單調(diào)遞減,則m的取值范圍是____________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在古裝電視劇《知否》中,甲乙兩人進行一種投壺比賽,比賽投中得分情況分“有初”“貫耳”“散射”“雙耳”“依竿”五種,其中“有初”算“兩籌”,“貫耳”算“四籌”,“散射”算“五籌”,“雙耳”算“六籌”,“依竿”算“十籌”,三場比賽得籌數(shù)最多者獲勝.假設(shè)甲投中“有初”的概率為![]() ,投中“貫耳”的概率為
,投中“貫耳”的概率為![]() ,投中“散射”的概率為
,投中“散射”的概率為![]() ,投中“雙耳”的概率為
,投中“雙耳”的概率為![]() ,投中“依竿”的概率為
,投中“依竿”的概率為![]() ,乙的投擲水平與甲相同,且甲乙投擲相互獨立.比賽第一場,兩人平局;第二場,甲投了個“貫耳”,乙投了個“雙耳”,則三場比賽結(jié)束時,甲獲勝的概率為( )
,乙的投擲水平與甲相同,且甲乙投擲相互獨立.比賽第一場,兩人平局;第二場,甲投了個“貫耳”,乙投了個“雙耳”,則三場比賽結(jié)束時,甲獲勝的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在三棱柱![]() 中,
中,![]() 是邊長為2的菱形,且
是邊長為2的菱形,且![]() ,
,![]() 是矩形,
是矩形,![]() ,且平面
,且平面![]() 平面
平面![]() ,
,![]() 點在線段
點在線段![]() 上移動(
上移動(![]() 不與
不與![]() 重合),
重合),![]() 是
是![]() 的中點.
的中點.
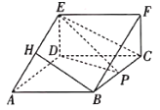
(1)當四面體![]() 的外接球的表面積為
的外接球的表面積為![]() 時,證明:
時,證明:![]() .平面
.平面![]()
(2)當四面體![]() 的體積最大時,求平面
的體積最大時,求平面![]() 與平面
與平面![]() 所成銳二面角的余弦值.
所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() .
.
(1)討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(2)記![]() 表示
表示![]() 中的最小值,設(shè)
中的最小值,設(shè)![]() ,若函數(shù)
,若函數(shù)![]() 至少有三個零點,求實數(shù)
至少有三個零點,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】北方的冬天戶外冰天雪地,若水管裸露在外,則管內(nèi)的水就會結(jié)冰從而凍裂水管,給用戶生活帶來不便.每年冬天來臨前,工作人員就會給裸露在外的水管“保暖”:在水管外面包裹保溫帶,用一條保溫帶盤旋而上一次包裹到位.某工作人員采用四層包裹法(除水管兩端外包裹水管的保溫帶都是四層):如圖1所示是相鄰四層保溫帶的下邊緣輪廓線,相鄰兩條輪廓線的間距是帶寬的四分之一.設(shè)水管的直徑與保溫帶的寬度都為4cm.在圖2水管的側(cè)面展開圖中,此保溫帶的輪廓線與水管母線所成的角的余弦值是( )(保溫帶厚度忽略不計)
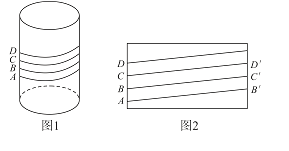
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】2019年慶祝中華人民共和國成立70周年閱兵式彰顯了中華民族從站起來、富起來邁向強起來的雄心壯志.閱兵式規(guī)模之大、類型之全均創(chuàng)歷史之最,編組之新、要素之全彰顯強軍成就.裝備方陣堪稱“強軍利刃”“強國之盾”,見證著人民軍隊邁向世界一流軍隊的堅定步伐.此次大閱兵不僅得到了全中國人的關(guān)注,還得到了無數(shù)外國人的關(guān)注.某單位有10位外國人,其中關(guān)注此次大閱兵的有8位,若從這10位外國人中任意選取3位做一次采訪,則被采訪者中至少有2位關(guān)注此次大閱兵的概率為( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某校高三年級有男生![]() 人,學(xué)號為
人,學(xué)號為![]() ,
,![]() ,
,![]() ,
,![]() ;女生
;女生![]() 人,學(xué)號為
人,學(xué)號為![]() ,
,![]() ,
,![]() ,
,![]() .對高三學(xué)生進行問卷調(diào)查,按學(xué)號采用系統(tǒng)抽樣的方法,從這
.對高三學(xué)生進行問卷調(diào)查,按學(xué)號采用系統(tǒng)抽樣的方法,從這![]() 名學(xué)生中抽取
名學(xué)生中抽取![]() 人進行問卷調(diào)查(第一組采用簡單隨機抽樣,抽到的號碼為
人進行問卷調(diào)查(第一組采用簡單隨機抽樣,抽到的號碼為![]() );再從這
);再從這![]() 名學(xué)生中隨機抽取
名學(xué)生中隨機抽取![]() 人進行數(shù)據(jù)分析,則這
人進行數(shù)據(jù)分析,則這![]() 人中既有男生又有女生的概率是( )
人中既有男生又有女生的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】南宋數(shù)學(xué)家楊輝在《詳解九章算法》和《算法通變本末》中,提出了一些新的垛積公式,所討論的高階等差數(shù)列與一般等差數(shù)列不同,前后兩項之差并不相等,但是逐項差數(shù)之差或者高次差成等差數(shù)列對這類高階等差數(shù)列的研究,在楊輝之后一般稱為“垛積術(shù)”.現(xiàn)有高階等差數(shù)列,其前7項分別為1,4,8,14,23,36,54,則該數(shù)列的第19項為( )(注:![]() )
)
A.1624B.1024C.1198D.1560
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com