
【題目】已知函數f(x)=x(1-![]() )是R上的偶函數.
)是R上的偶函數.
(1)對任意的x∈[1,2],不等式m·![]() ≥2x+1恒成立,求實數m的取值范圍.
≥2x+1恒成立,求實數m的取值范圍.
(2)令g(x)=1-![]() ,設函數F(x)=g(4x-n)-g(2x+1-3)有零點,求實數n的取值范圍.
,設函數F(x)=g(4x-n)-g(2x+1-3)有零點,求實數n的取值范圍.
【答案】(1)實數m的取值范圍為[3,+∞).(2)實數n的取值范圍是(2,+∞).
【解析】試題分析:(1)先根據偶函數得a=2,再分離變量得m≥2x-1最大值,即得實數m的取值范圍(2)根據函數單調性化簡方程F(x)=0得n=4x-2x+1+3,再根據二次函數值域求實數n的取值范圍.
試題解析:(1)∵函數f(x)為偶函數,∴f(-x)=f(x),即(-x)·(1-![]() )=x·(1-
)=x·(1-![]() ).
).
∴x·(2-a)=0,由于x不恒為0,∴a=2.3分
故f(x)=x(1-![]() )=x·
)=x·![]() .
.
又x∈[1,2],∴2x-1>0,2x+1>0,
∴不等式m·![]() ≥2x+1恒成立,等價于m≥2x-1恒成立.
≥2x+1恒成立,等價于m≥2x-1恒成立.
又x∈[1,2],∴2x-1∈[1,3],∴當m≥3時,不等式m≥2x-1恒成立,
∴實數m的取值范圍為[3,+∞).
(2)函數F(x)=g(4x-n)-g(2x+1-3)有零點,等價于方程g(4x-n)-g(2x+1-3)=0有實數根.由(1)知f(x)=x(1-![]() ),
),
∴g(x)=1-![]() =
=![]() (x≠0).
(x≠0).
由2x+1是增函數,∴g(x)是減函數.9分
∴4x-n=2x+1-3,
∴n=4x-2x+1+3.
∵4x-2x+1+3
=(2x)2-2·2x+3
=(2x-1)2+2,
又x≠0,∴(2x-1)2+2>2.
故實數n的取值范圍是(2,+∞).


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】設函數f(x)=ex-ax-1.
(1)當a>0時,設函數f(x)的最小值為g(a),求證:g(a)≤0;
(2)求證:對任意的正整數n,都有1n+1+2n+1+3n+1+…+nn+1<(n+1)n+1.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于給定的正整數![]() ,如果各項均為正數的數列
,如果各項均為正數的數列![]() 滿足:對任意正整數
滿足:對任意正整數![]() ,
,
![]() 總成立,那么稱
總成立,那么稱![]() 是“
是“![]() 數列”.
數列”.
(1)若![]() 是各項均為正數的等比數列,判斷
是各項均為正數的等比數列,判斷![]() 是否為“
是否為“![]() 數列”,并說明理由;
數列”,并說明理由;
(2)若![]() 既是“
既是“![]() 數列”,又是“
數列”,又是“![]() 數列”,求證:
數列”,求證: ![]() 是等比數列.
是等比數列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=![]() 在點(1,1)處的切線方程為x+y=2.
在點(1,1)處的切線方程為x+y=2.
(1)求a,b的值;
(2)對函數f(x)定義域內的任一個實數x,不等式f(x)-![]() <0恒成立,求實數m的取值范圍.
<0恒成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
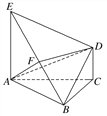
【題目】如圖所示,底面ABC為正三角形,EA⊥平面ABC,DC⊥平面ABC,EA=AB=2DC=2a,設F為EB的中點.
(1)求證:DF∥平面ABC;
(2)求直線AD與平面AEB所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】心理學家發現視覺和空間能力與性別有關,某數學興趣小組為了驗證這個結論,從興趣小組中按分層抽樣的方法抽取50名同學,給所有同學幾何和代數各一題,讓各位同學自由選擇一道題進行解答.統計情況如下表:(單位:人)
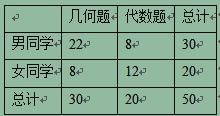
(1)能否據此判斷有![]() 的把握認為視覺和空間能力與性別有關?
的把握認為視覺和空間能力與性別有關?
(2)經過多次測試發現:女生甲解答一道幾何題所用的時間在5—7分鐘,女生乙解答一道幾何題所用的時間在6—8分鐘,現甲、乙兩人獨立解答同一道幾何題,求乙比甲先解答完的概率;
(3)現從選擇幾何題的8名女生中任意抽取兩人對她們的答題情況進行研究,記甲、乙兩名女生被抽到的人數為![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
附表及公式

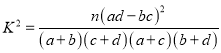
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=xlnx和g(x)=m(x2-1)(m∈R).
(1)m=1時,求方程f(x)=g(x)的實根;
(2)若對任意的x∈(1,+∞),函數y=g(x)的圖象總在函數y=f(x)圖象的上方,求m的取值范圍;
(3)求證: ![]() +
+![]() +…+
+…+![]() >ln(2n+1) (n∈N*).
>ln(2n+1) (n∈N*).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com