Question

【題目】已知函數(shù)，.

（1）若函數(shù)在處的切線與直線平行，求實數(shù)的值；

（2）試討論函數(shù)在區(qū)間上最大值；

（3）若時，函數(shù)恰有兩個零點，求證：.

Answer 1

【答案】(1);(2) 當(dāng)時,,當(dāng)時，;(3)見解析.

【解析】

試題分析：(1)求函數(shù)的導(dǎo)數(shù)，由求之即可；(2) ，分當(dāng)與分別討論函數(shù)的單調(diào)性，求其最值即可；(3)由可得，即，設(shè)，則，即，故，用作差比較法證明即可.

試題解析： （1）由，，

由于函數(shù)在處的切線與直線平行，

故，解得.

（2），由時，；時，，

所以①當(dāng)時，在上單調(diào)遞減，

故在上的最大值為；

②當(dāng)，在上單調(diào)遞增，在上單調(diào)遞減，

故在上的最大值為；

（3）若時，恰有兩個零點，

由，，

得，

∴，設(shè)，，，

故，

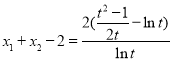∴，記函數(shù)，因，

∴在遞增，∵，∴，

又，，故成立.